Kezdőlap


Feladat:	F.3116	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bérczi Gergely , Czirok Levente , Gerő Tamás Miklós , Gyenes Zoltán , Gyukics Mihály , Makai Márton , Pápay Mihály , Prause István , Szabó Jácint , Szobonya László , Tollas Ágnes , Vörös Zoltán , Zábrádi Zoltán , Zaupper Bence
Füzet:	1996/december, 536 - 538. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Beírt alakzatok, Hossz, kerület, Háromszögek hasonlósága, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1996/március: F.3116

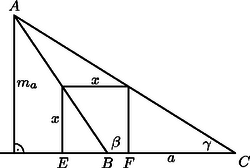
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az 1. ábra hasonló háromszögeiből

\frac{a}{x} = \frac{m_{a}}{m_{a} - x}

, és ebből

x = \frac{a \cdot m_{a}}{a + m_{a}}

. Ezután

\frac{a}{x} = \frac{a + m_{a}}{m_{a}} = 1 + \frac{a}{m_{a}}

. A háromszög területe

t = \frac{a \cdot m_{a}}{2}

, így

\frac{a}{x} = 1 + \frac{a^{2}}{2 t}

. Hasonlóan kapjuk, hogy

\frac{b}{y} = 1 + \frac{b^{2}}{2 t}

és

\frac{c}{z} = 1 + \frac{c^{2}}{2 t}

. Ezért a bizonyítandó állítás:

\begin{matrix} 1 + \frac{a^{2}}{2 t} + 1 + \frac{b^{2}}{2 t} + 1 + \frac{c^{2}}{2 t} \geq 3 + 2 \sqrt[]{3}, \end{matrix}

azaz

a^{2} + b^{2} + c^{2} \geq 4 t \sqrt[]{3}

. Ehelyett elegendő azt bizonyítani, hogy

\begin{matrix} {(a^{2} + b^{2} + c^{2})}^{2} \geq 16 \cdot t^{2} \cdot 3. \end{matrix}

(1)

Ezt a következőképpen igazolhatjuk. A koszinusztétel szerint

\begin{matrix} cos γ = \frac{a^{2} + b^{2} - c^{2}}{2 a b}, amiből sin^{2} γ = 1 - \frac{{(a^{2} + b^{2} - c^{2})}^{2}}{4 a^{2} b^{2}}, \end{matrix}

a háromszög területének négyzete pedig

\begin{matrix} t^{2} = \frac{a^{2} b^{2}}{4} [1 - \frac{{(a^{2} + b^{2} - c^{2})}^{2}}{4 a^{2} b^{2}}] = \frac{4 a^{2} b^{2} - {(a^{2} + b^{2} - c^{2})}^{2}}{16} . \end{matrix}

Ezt (1)-be helyettesítve:

\begin{matrix} {(a^{2} + b^{2} + c^{2})}^{2} \geq 3 [4 a^{2} b^{2} - {(a^{2} + b^{2} - c^{2})}^{2}] . \end{matrix}

Ebből néhány átalakitással

\begin{matrix} {(a^{2} - b^{2})}^{2} + {(b^{2} - c^{2})}^{2} + (c^{2} - a^{2}) \geq 0, \end{matrix}

(2)

ami nyilvánvalóan fennáll. Mivel egyenlőtlenségeink egymással ekvivalensek, a feladat állítását igazoltuk. (2)-ben, és a bizonyítandó egyenlőtlenségben is pontosan akkor áll fenn egyenlőség, ha

a = b = c

, tehát szabályos háromszög esetén.

Pápay Mihály (Szolnok, Verseghy F. Gimn., IV. o.t.) és

Zábrádi Zoltán (Győr, Czuczor G. Bencés Gimn., IV. o.t.)

II. megoldás. Az 1. ábra jelöléseivel

a = B E + E F + F C = x (1 + ctg β + ctg γ)

, tehát

\frac{a}{x} = 1 + ctg β + ctg γ

. Hasonlóan kapjuk:

\frac{b}{y} = 1 + ctg α + ctg γ

\frac{c}{z} = 1 + ctg α + ctg β

. A három egyenletet összeadva:

\begin{matrix} \frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 3 + 2 (ctg α + ctg β + ctg γ) . \end{matrix}

A kotangens egyenlőtlenség szerint

\begin{matrix} ctg α + ctg β + ctg γ \geq \sqrt[]{3}, \end{matrix}

(3)

amiből már következik a feladat állítása.
A (3) egyenlőtlenséget a következőképpen igazolhatjuk. Mivel a feladat szigorú ,,beírási'' előírása szerint a négyzetcsúcsok az oldalakra illeszkednek, a háromszög szögeire

0 < α, β, γ \leq 90^{\circ}

. Mivel a

ctg x

függvény a

(0; 90^{\circ}]

intervallumon konvex, a Jensen-egyenlőtlenség szerint

ctg α + ctg β + ctg γ \geq 3 \cdot ctg \frac{α + β + γ}{3} = \sqrt[]{3}

Prause István (Budapest, Piarista Gimn., III. o.t.) és

Zaupper Bence (Győr, Krúdy Gy. Szki., IV. o.t.)

Megjegyzések. 1. A feladat állítása akkor is igaz, ha a ,,beírt'' négyzetekre csak azt kívánjuk meg, hogy csúcsaik az oldalegyenesekre illeszkedjenek. A 2. ábra alapján láthatjuk, hogy az I. megoldásban pl. az

\frac{a}{x}

számítása szóról-szóra átvihető tompaszögű háromszögre. A II. megoldásban pl. az

a

oldal meghatározása a következő lesz:

\begin{matrix} \begin{matrix} a = E F + F C - E B = \\ = x + x \cdot ctg γ - x \cdot ctg (180^{\circ} - β) = \\ = x (1 + ctg β + ctg γ), \end{matrix} \end{matrix}

tehát nincs változás. Természetesen a (3) egyenlőtlenség is igazolható tetszőleges háromszögre (lásd a következő megjegyzést). Derékszögű háromszög esetén a három négyzet közül kettő egybeesik.
2. A bemutatott két megoldás szoros kapcsolatban áll. Ismeretes, hogy a háromszög területe a következő összefüggésből is kiszámítható:

\begin{matrix} a^{2} + b^{2} + c^{2} = 4 t \cdot (ctg α + ctg β + ctg γ) . \end{matrix}

(4)

(Lásd. pl. Reiman I.: A geometria és határterületei c. könyve 69. old.)
Egyszerű számolással igazolható, hogy (4) oldalai nem kisebbek, mint

4 t \sqrt[]{3}

, azaz

a^{2} + b^{2} + c^{2} \geq 4 t \sqrt[]{3}

, illetve

4 t (ctg α + ctg β + ctg γ) \geq 4 t \sqrt[]{3}

, tehát

ctg α + ctg β + ctg γ \geq \sqrt[]{3}

(lásd a feljebb idézett mű 236‐237. oldalát). Ez azt mutatja, hogy a két különbözőnek látszó megoldás eszköze közös eredetű.