Feladat:	F.3109	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Barát Anna ,  Bérczi Gergely ,  Braun Gábor ,  Cheri Enikő ,  Gyenes Zoltán ,  Gyukics Mihály ,  Hans Zoltán ,  Harrach Nóra Viola ,  Kiss Ádám ,  Kiss László ,  Kocsis Zoltán ,  Nagy Margit ,  Pap Júlia ,  Pintér Dömötör ,  Rozmán András ,  Salamon Gábor ,  Szántó Richárd ,  Szobonya László ,  Terék Zsolt ,  Tóth Ádám ,  Vaszil Krisztina
Füzet:	1996/december, 531 - 533. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek nevezetes tételei, Terület, felszín, Vektorok vektoriális szorzata, Paralelogrammák, Feladat
Hivatkozás(ok):	Feladatok: 1996/február: F.3109

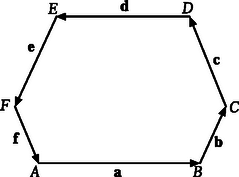
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Tekintsük a hatszög oldalvektorait az 1. ábra szerinti irányítással. Jelöljük pl. az $ACE▵$ területét $t_{ACE}$-vel. A vektoriális szorzat definíciója szerint (lásd pl. Reiman István: A geometriai és határterületei c. könyvének 46. oldalán): $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 2t_{ACE}}& {\displaystyle =\left|\left(\text{c}+\text{d}\right)\times \left(-\text{a}-\text{b}\right)\right|}\hfill \\ \multicolumn{3}{c}{\text{<br>és}}\\ \hfill {\displaystyle 2t_{BDF}}& {\displaystyle =\left|\left(\text{d}+\text{e}\right)\times \left(-\text{b}-\text{c}\right)\right|\mathrm{.}}\hfill \end{array}}}\end{array}$ Tekintve, hogy mindkét vektoriális szorzat ugyanolyan irányú, elegendő azt bizonyítani, hogy $\begin{array}{c}{\displaystyle \left(\text{c}+\text{d}\right)\times \left(-\text{a}-\text{b}\right)=\left(\text{d}+\text{e}\right)\times \left(-\text{b}-\text{c}\right)\mathrm{.}}\end{array}$ (1) A vektoriális szorzat tulajdonságai szerint (1) így alakítható: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(\text{a}+\text{b}\right)\times \left(\text{c}+\text{d}\right)=\left(\text{b}+\text{c}\right)\times \left(\text{d}+\text{e}\right)\mathrm{,}}\\ \hfill {\displaystyle \text{a}\times \text{c}+\text{b}\times \text{c}+\text{a}\times \text{d}+\text{b}\times \text{d}=\text{b}\times \text{d}+\text{c}\times \text{d}+\text{b}\times \text{e}+\text{c}\times \text{e}\mathrm{,}}\end{array}}}\end{array}$ ebben $\text{b}\times \text{d}$ mindkét oldalon szerepel, továbbá $\text{a}\times \text{d}=\text{b}\times \text{e}=\text{0}$, ezért azt kell megmutatni, hogy $\begin{array}{c}{\displaystyle \text{a}\times \text{c}+\text{b}\times \text{c}-\text{c}\times \text{d}-\text{c}\times \text{e}=\mathrm{0,}\text{azaz}\left(\text{a}+\text{b}+\text{d}+\text{e}\right)\times \text{c}=\text{0}\mathrm{.}}\end{array}$ Ez pedig nyilván igaz, hiszen $\text{a}+\text{b}+\text{c}+\text{e}=-\text{c}-\text{f}$, és ez párhuzamos a $\text{c}$-vel. Mivel átalakításaink megfordíthatók, igaz a feladat állítása. Nyilvánvaló, hogy megoldásunk nemcsak konvex, hanem bármilyen, a feltételeknek megfelelő hatszögre alkalmazható, azaz a hatszög lehet akár hurkolt, vagy akár nem síkbeli hatszög is.  Gyukics Mihály (Szolnok, Varga Katalin Gimn., IV. o.t.) és    Kiss László (Fazekas M. Főv. Gyak. Gimn., III. 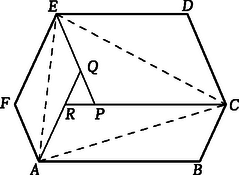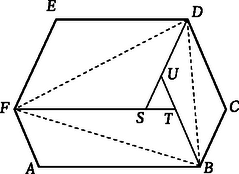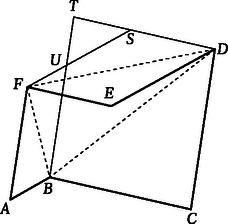o.t.) dolgozata alapján   II. megoldás. A 2. ábrán egy konvex hatszög van. Ennek $A$, $B$, $C$ csúcsai és az $R$ pont egy $AC$ átlójú paralelogrammát határoz meg. Hasonlóan szerkesztettük a $CE$ átlójú $CDEP$, illetve az $EA$ átlójú $EFAQ$ paralelogrammát. A 3. ábra paralelogrammái úgy készültek, hogy egy-egy átlójuk a $BD$, $DF$, illetve az $FB$ szakasz, tehát a $BDF▵$ oldalai, és a paralelogrammáknak a hatszögcsúcsoktól különböző csúcsai $S$, $T$, $U$. Könnyen látható, hogy $RP=ST=AB-ED$, és hasonlóan $PQ=TU$ és $QR=US$. Ezért $RPQ▵\cong STU▵$, tehát $t_{RPQ}=t_{STU}$, amely állítás akkor is igaz, ha az $R$, $P$ $Q$, illetve az $S$, $T$, $U$ pontok egybeesnek. Ez azt is jelenti, hogy a 3‐3 paralelogramma területösszege egyenlő. Ennek folytán az $ACE▵$ területe is, és a $BDF▵$ területe is a megfelelő paralelogrammák félterületének és a köztük lévő háromszög területének az összege, és ez a két esetben egyenlő. 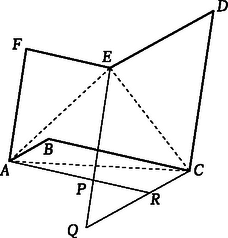Ha a hatszögnek van ${180}^{\circ }$-nál nagyobb szöge, akkor két ilyen is van. Ilyen konkáv hatszöget látunk a 4. és 5. ábrán. Könnyen leolvasható, hogy a $t_{CDEQ}+t_{EFAP}-t_{ABCR}-t_{RPQ}$ és a $t_{BCDT}+t_{ABUF}-t_{FEDS}-t_{STU}$ területek egyenlőek, és $t_{RPQ}=t_{STU}$, ezért $\frac{1}{2}\left(t_{CDEQ}+t_{EFAP}-t_{ABCR}\right)-t_{RPQ}=\frac{1}{2}\left(t_{BCDT}+t_{ABUF}-t_{FEDS}\right)-t_{STU}$. utóbbi éppen azt jelenti, hogy $t_{ACE}=t_{BDF}$. Hasonlóan járhatunk el hurkolt hatszög esetén is.  Tóth Ádám (Fazekas M. Főv. Gyak. Gimn., II. o.t.) dolgozata alapján