Feladat: C.427 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Méder Áron 
Füzet: 1996/október, 407. oldal  PDF  |  MathML 
Témakör(ök): Érintőnégyszögek, Trapézok, Pitagorasz-tétel alkalmazásai, Alakzatba írt kör, C gyakorlat
Hivatkozás(ok):Feladatok: 1996/március: C.427

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Rajzoljunk először egy tetszőleges trapézt. Hosszabbik párhuzamos oldala AB=a, rövidebbik párhuzamos oldala CD=b. Fejezzük ki az átlók metszéspontján átmenő, az alapokkal párhuzamos szakasz hosszát a-val és b-vel.
Jelölje az átlók metszéspontját O, a párhuzamos és AD metszéspontja E, CB-vel való metszéspontja F, és legyen G az AB szakasz azon pontja, amelyre CG‖AD.
Az AOB▵∼COD▵-ből ABCD=ab=mamb; az EF és CG szakasz metszéspontját H-val jelölve, a CGB▵∼CHF▵-ből HFGB=mbma+mb, innen HF=GB⋅mbma+mb.
EF=EH+HF=b+GB⋅mbma+mb=b+(a-b)ba+b=2aba+b.

Az előbb kapott eredményt alkalmazzuk a feladatban adott derékszögű érintő trapézra. Így azt kell most igazolnunk, hogy
EF=2aba+b=m.
A trapézba írt kör sugara r, és AD=2r=m. Az érintőnégyszögben a szemközti oldalak összege egyenlő, azaz
CB+AD=CB+m=a+b,
ahonnan CB=a+b-m.
A BCG derékszögű háromszögben
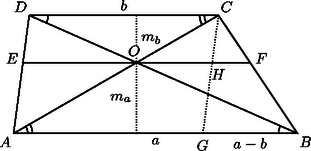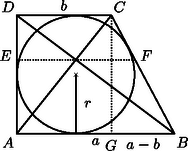(a+b-m)2=(a-b)2+m2.
Négyzetreemelés és rendezés után kapjuk, hogy
m=2aba+b,
s ezt akartuk bizonyítani.
 Méder Áron (Budapest, Táncsics M. Gimn., II. o.t.)