Legyen $XYZ$ egy olyan szabályos háromszög, amelynek $XY$ oldala $C$-re, $YZ$ oldala $A$-ra, $ZX$ oldala pedig $B$-re illeszkedik. Mivel a szabályos háromszögek egymáshoz   hasonlóak, ezért $XYZ$ területe akkor a lehető legnagyobb, ha oldala ‐ pl. $YZ$ ‐ a lehető legnagyobb.
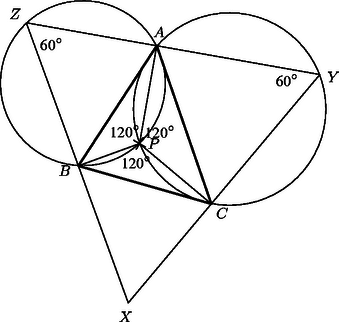
Mivel $Z$-ből az $AB$ szakasz ${60}^{\circ }$-os szögben látszik, ezért $Z$ rajta van az $AB$ szakaszhoz tartozó ${60}^{\circ }$-os látóköríven. Ugyanígy $Y$ rajta van az $AC$ szakaszhoz tartozó ${60}^{\circ }$-os látóköríven, A két látókörívet tartalmazó körök $A$-tól különböző metszéspontja legyen $P$. Mivel $ABC$ hegyesszögű, ezért $P$ az $ABC$ háromszög belső pontja (1. ábra), továbbá
$APB\sphericalangle ={180}^{\circ }-AZB\sphericalangle ={120}^{\circ }$,
$APC\sphericalangle ={180}^{\circ }-AYC\sphericalangle ={120}^{\circ }$,
és ezért $BPC\sphericalangle ={360}^{\circ }-$
-APB∢-APC∢=120∘. ($P$ az $ABC$ háromszög ún. izogonális pontja, az a pont, amelyből a háromszög mindhárom oldala ugyanakkora szögben látszik.)
Megmutatjuk, hogy $YZ$ akkor maximális, ha merőleges $AP$-re.
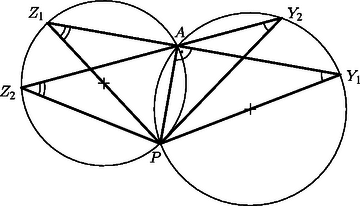
Legyenek $Y_1{Z}_1$ az $AP$-re merőleges, $Y_2{Z}_2$ pedig egy $AP$-re nem merőleges, $A$-n átmenő szakaszok, amelyek végpontjai az $AC$, illetve az $AB$ szakasznak ${60}^{\circ }$-os látókörívén vannak (2. ábra). 
Ekkor $A{Y}_{1}P\sphericalangle =A{Y}_{2}P\sphericalangle$ és $A{Z}_{1}P\sphericalangle =A{Z}_{2}P\sphericalangle$, mivel azonos íven nyugvó kerületi szögek. Emiatt a $Z_1{Y}_{1}P$ és a $Z_2{Y}_{2}P$ háromszögek hasonlóak. Mivel $PA{Y}_1\sphericalangle ={90}^{\circ }$, ezért $P{Y}_1$ a kör átmérője, tehát $P{Y}_1>P{Y}_2$ (ugyanígy $P{Z}_1$ is átmérő a másik látókörben). Hasonló háromszögekben a megfelelő oldalak aránya megegyezik, így $Y_1{Z}_1>Y_2{Z}_2$.
Ezek alapján a szerkesztést a következőképpen végezhetjük: Az $AB$ és az $AC$ oldalakra ‐ kifelé ‐ szabályos háromszögeket szerkesztünk, majd a háromszögek körülírt köreit is megszerkesztjük. A két kör $A$-tól különböző metszéspontja $P$. Az $AP$-re $A$-ban állított merőleges és a két kör második metszéspontjai $Y$ és $Z$. A $ZB$ és $YC$ egyenesek metszéspontja $X$. Az így szerkesztett $XYZ$ háromszög szabályos, mert $AYC\sphericalangle =AZB\sphericalangle ={60}^{\circ }$ (a szerkesztés miatt), ezért $BXC\sphericalangle$ is ${60}^{\circ }$-os. Területe a lehető legnagyobb, mert a fenti bizonyításból következik, hogy $YZ$ hossza maximális.