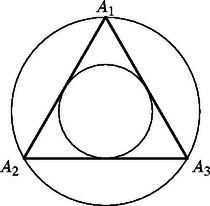
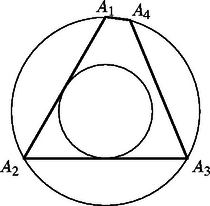
Ha egy szabályos háromszög csúcsai a nagyobbik körön vannak, akkor beírt köre éppen a kisebbik kör (1. ábra). Az ilyen tulajdonságú szabályos háromszögek területe $3\sqrt[]{3}$ területegység. Megmutatjuk, hogy ha az $A_1{A}_2\text{...}{A}_n$ sokszög tartalmazza a kisebbik kört, csúcsai pedig a nagyobbik körön vannak, akkor a területe legalább $3\sqrt[]{3}$.
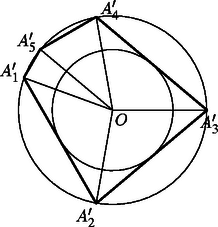
$|A_1{A}_2|=|A_1\text{'}{A}_2\text{'}|$;  $|A_3{A}_4|=|A_2\text{'}{A}_3\text{'}|$;  $|A_4{A}_5|=|A_3\text{'}{A}_4\text{'}|$;  $|A_2{A}_3|=|A_4\text{'}{A}_5\text{'}|$;  $|A_5{A}_1|=|A_5\text{'}{A}_1\text{'}|$ 2. ábra
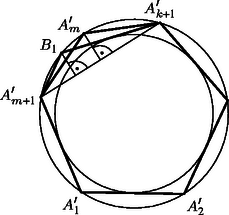
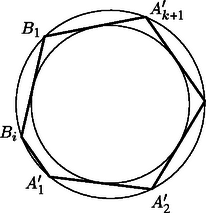
Tekintsünk most két tetszőleges sugarú koncentrikus kört, és legyen a nagyobbikba írt sokszög, amelyik tartalmazza a kisebb kört, $A_1{A}_2\text{...}{A}_n$. Jelöljük a körök középpontját $O$-val. A sokszög területe megegyezik az $A_{i}O{A}_{i+1}$ ($i=1$, $2$, $\text{...}$ $n$; $A_{n+1}=A_1$) háromszögek területeinek összegével. Ez a területösszeg nyilván nem változik, ha a háromszögek sorrendjét megváltoztatjuk. Rakjuk egymás mellé azokat a háromszögeket, amelyek $A_i{A}_{i+1}$ oldala érinti a kisebbik kört, majd ezután változtassuk meg a csúcsok betűzését úgy, hogy az $A_1\text{'}{A}_2\text{'}$, $A_2\text{'}{A}_3\text{'}$, $\text{...}$, $A_k\text{'}{A}_{k+1}\text{'}$ oldalak legyenek azok, amelyek érintik a kisebbik kört; az $A_{k+1}\text{'}$, $A_{k+2}\text{'}$, $\text{...}$, $A_n\text{'}$, $A_1\text{'}$ oldalak pedig azok, amelyek nem érintik (a 2. ábrán ezt láthatjuk ötszög esetén). Az így kapott $A_1\text{'}{A}_2\text{'}\text{...}{A}_n\text{'}$ sokszög területe megegyezik az eredeti $A_1{A}_2\text{...}{A}_n$ sokszög területével. Vizsgáljuk most az $A_{k+1}\text{'}{A}_{k+2}\text{'}$, $A_{k+1}\text{'}{A}_{k+3}\text{'}$, $\text{...}$, $A_{k+1}\text{'}{A}_n\text{'}$, $A_{k+1}\text{'}{A}_1\text{'}$ egyeneseket. Legyen ezek közül ‐ ilyen sorrendben ‐ $A_{k+1}\text{'}{A}_{m+1}\text{'}$ az első olyan, amelyik metszi a kisebbik kört. Ekkor az $A_{k+1}\text{'}$-ből a kisebbik körhöz húzott $A_k\text{'}{A}_{k+1}\text{'}$-tól különböző érintőnek a nagy körrel való $A_{k+1}\text{'}$-től különböző metszéspontját jelöljük $B_1$-gyel (3. ábra). Az $A_{k+1}\text{'}{A}_{m+1}\text{'}{B}_1$ háromszög területe kisebb, mint az $A_{k+1}\text{'}{A}_{m+1}\text{'}{A}_m\text{'}$ háromszög területe, mert $B_1$ közelebb van az $A_{k+1}\text{'}{A}_{m+1}\text{'}$ egyeneshez, mint $A_m\text{'}$ (ugyanis $A_{k+1}\text{'}{A}_m\text{'}$ és $A_m\text{'}{A}_{m+1}\text{'}$ nem metszhetik a kis kört). Tehát az $A_1\text{'}{A}_2\text{'}\text{...}{A}_{k+1}\text{'}{B}_1{A}_{m+1}\text{'}{A}_{m+2}\text{'}\text{...}{A}_n\text{'}$ sokszög területe kisebb, mint az $A_1\text{'}{A}_2\text{'}\text{...}{A}_n\text{'}$ sokszög területe. Ezután ismételjük meg ezt a ,,levágási'' eljárást úgy, hogy $A_{k+1}\text{'}$ szerepét $B_1$ veszi át. Véges sok vágás után ‐ az új pontokat rendre $B_2$, $B_3$, $\text{...}$, $B_i$-vel jelölve ‐ elérjük, hogy a $B_i{A}_1\text{'}$ egyenes még nem metszi (esetleg érinti), a $B_i{A}_2\text{'}$ egyenes viszont metszi a kis kört. A kapott $A_1\text{'}{A}_2\text{'}\text{...}{A}_{k+1}\text{'}{B}_1{B}_2\text{...}{B}_i$ sokszög az egybevágóság erejéig egyértelmű, ezért az eljárásból következően ez a legkisebb területű azon sokszögek közül, melyek tartalmazzák a kis kört, csúcsaik pedig a nagy körön vannak. Ezt a sokszöget azzal jellemezhetjük, hogy ‐ legfeljebb egy oldala ($B_i{A}_1\text{'}$) kivételével ‐ mindegyik oldala érinti a kis kört (4. ábra). Ez a tulajdonság a két kör sugarának arányától függetlenül mindig igaz a minimális területű sokszögre.
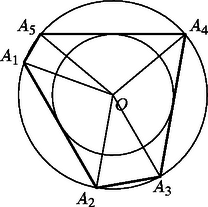
Visszatérve eredeti feladatunkra, ha a két kör sugara 1, illetve 2, akkor éppen a nagy körbe írható szabályos háromszöget kapjuk, mint a követelményeket kielégítő, minimális területű sokszöget. Ha $A_1{A}_2{A}_3$ egy a nagy körbe írt szabályos háromszög, $A_4$ pedig a rövidebbik $A_3{A}_1$ ív egy $A_1$-hez ,,közel'' lévő pontja, akkor az $A_1{A}_2{A}_3{A}_4$ húrnégyszög (5. ábra) területe nagyobb, mint az $A_1{A}_2{A}_3$ háromszög területe, de tetszőlegesen megközelítheti azt. Tehát a nagyobbik körbe írt és a kisebbik kört tartalmazó húrnégyszögek területe nagyobb mint $3\sqrt[]{3}$, de tetszőlegesen megközelítheti ezt az értéket.