Kezdőlap


Feladat:	Gy.3001	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bakonyi Gábor , Bérczi Gergely , Egri Győző , Jakabfy Tamás , Juhász András , Naszódi Anna , Nyakas Péter , Reviczky Ágnes , Röst János , Schlotter Ildikó , Szilágyi Jenő , Szita István
Füzet:	1996/március, 157 - 159. oldal		PDF \| MathML
Témakör(ök):	Sakktáblával kapcsolatos feladatok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1995/szeptember: Gy.3001

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzés. A megoldás során szomszédosnak olyan mezőket nevezünk, amelyek élben vagy csúcsban csatlakoztak egymáshoz. Amennyiben csak az élben csatlakozást tekintenénk, a feladat triviálisan megoldható lenne (pl. egy-egy sorba minden második helyre csupa sötét, ill. csupa világos figurát téve). Akik így oldották meg a feladatot, nem kaptak pontot.

Megoldás. A közölt megoldásban a következő, általánosabb állítást fogjuk igazolni: ha

n > 2

n \neq 4 k + 2

, akkor az

n \times n

-es sakktáblára fel lehet állítani

[\frac{n^{2}}{2}]

bábut úgy, hogy ezeknek a fele sötét, a fele világos, és minden figurának ugyanannyi világos szomszédja van, mint sötét, míg

n = 4 k + 2

-re

[\frac{n^{2}}{2}] + 2

számút, illetve erre mutatunk egy

[\frac{n^{2}}{2}] - 2

-es elhelyezést is.
Először igazoljuk azt, hogy

[\frac{n^{2}}{2}]

mindig páros: ha

n = 2 k

, akkor

[\frac{n^{2}}{2}] = 2 k^{2}

, míg

n = 2 k + 1

esetén

[\frac{n^{2}}{2}] = [\frac{4 k^{2} + 4 k + 1}{2}] = 2 k^{2} + 2 k

, mindkét esetben páros az eredmény. Ezek után megadunk egy-egy elhelyezési módot az

n = 3

, 4, 5, 6 esetekre (1. ábra):
Ha

n > 6

, akkor az

n \times n

-es problémát visszavezetjük egy

(n - 4) \times (n - 4)

-es elhelyezésre. A széleken levő mezőkre (a sarkok kivételével) felváltva két sötét és két világos bábut teszünk (akárcsak az 1. ábra 2. és 5. tábláján): ez lehetséges, hiszen összesen

4 (n - 2)

helyünk van. A következő ,,egy szélességű keretbe'' nem teszünk bábut, majd a fennmaradó

(n - 4) \times (n - 4)

-es táblára elhelyezünk

[\frac{{(n - 4)}^{2}}{2}]

, illetve

[\frac{{(n - 4)}^{2}}{2}] \pm 2

bábut. Amennyiben

n - 4 > 6

, akkor ismét egy kettő szélességű keretet töltünk be, és utána az

(n - 8) \times (n - 8)

-as tábla elrendezését használjuk. Nyilvánvaló, hogy a bábuk elhelyezése így megfelelő.
Egyetlen dolog szorul már csak bizonyításra: az, hogy az

n \times n

-es táblára valóban annyi bábut tettünk, mint amennyit kellett. Ehhez azt szükséges megmutatni, hogy

\begin{matrix} [\frac{n^{2}}{2}] = [\frac{{(n - 4)}^{2}}{2}] + 4 (n - 2) \end{matrix}

fennáll. Az

n = 2 k

esetben:

\begin{matrix} [\frac{{(2 k - 4)}^{2}}{2}] + 4 (2 k - 2) = 2 {(k - 2)}^{2} + 4 (2 k - 2) = 2 k^{2} - 8 k + 8 + 8 k - 8 = 2 k^{2} = [\frac{{(2 k)}^{2}}{2}], \end{matrix}

míg az

n = 2 k + 1

esetben:

\begin{matrix} [\frac{{(2 k - 3)}^{2}}{2}] + 4 (2 k - 1) = 2 k^{2} - 6 k + 4 + 4 (2 k - 1) = 2 k^{2} + 2 k = [\frac{{(2 k + 1)}^{2}}{2}] . \end{matrix}

Ezzel állításunkat igazoltuk.
A teljesség kedvéért a dolgozatokból lássunk néhány konkrét elhelyezést az

n = 8

esetben (2. ábra):
(Aki legalább egy jó elhelyezést mutatott, megkapta az 5 pontot.)
A 2. ábra legutolsó rajzának kis módosításával látható, hogy még 34 bábu is elhelyezhető. (Esetleg több is?) Egyébként a kitűzéssel egyidőben megjelent ,,Királyok körei'' című cikkből kiderül, hogy nem adható meg olyan megoldás, ahol a bábuk egyetlen zárt láncot alkotnak.

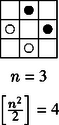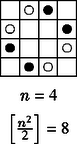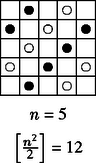Szita István (Körmend, Kölcsey F. Gimn., III. o.t.)

Nyakas Péter (Zalaegerszeg, Zrínyi M. Gimn., III. o.t.) dolgozata alapján