Kezdőlap


Feladat:	Gy.2988	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barát Anna , Barcza Gergely , Bérczi Gergely , Boja Bence , Deli Tamás , Formanek Csaba , Gáspár László , Hans Zoltán , Klausz Krisztián , Lénárt Zoltán , Lippner Gábor , Mátrai Tamás , Megyeri Csaba , Miszkuj Tünde , Molnár-Sáska Balázs , Nagy Ilona , Nyul Gábor , Pap Gyula , Pap Júlia , Pintér Dömötör , Pogány Ádám , Puskás Péter , Reviczky Ágnes , Ritz Attila , Simon Barna , Szabó Anett , Szabó Gábor , Székely László , Szepesi Zoltán , Szépszó Gabriella , Szilágyi Judit , Vörös Imre
Füzet:	1996/január, 22 - 23. oldal		PDF \| MathML
Témakör(ök):	Kör geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1995/április: Gy.2988

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük $R S$ és $F B$ metszéspontját $H$ -val, $k$ középpontját $O$ -val, $P Q$ , illetve $R S$ felezőpontját pedig $F_{1}$ -gyel, illetve $F_{2}$ -val (1. ábra). A $P Q F$ és az $S R F$ háromszögek hasonlóak, mert $P Q F ∢ = S R F ∢$ és $Q P F ∢ = R S F ∢$ (egy ívhez tartozó kerületi szögek). Ezért a két háromszögben a megfelelő oldalak aránya megegyezik, így

\begin{matrix} \frac{F Q}{Q P} = \frac{F R}{R S}, \end{matrix}

amiből

\begin{matrix} \frac{F Q}{F R} = \frac{Q P}{R S} = \frac{Q F_{1}}{R F_{2}} . \end{matrix}

Vagyis az

F_{1} F Q

és az

F_{2} F R

háromszögek is hasonlóak, mert megegyeznek két oldal arányában és az azok által bezárt szögben. Tehát

Q F_{1} F ∢ = R F_{2} F ∢

. Jelöljük ezt a szöget

α

-val.
Egy kör húrjának felezőpontját a kör középpontjával összekötő egyenes merőleges a húrra, ezért

O F_{1} N ∢ = O F N ∢ = O F_{2} H ∢ = O F H ∢ = 90^{\circ}

. Így az

O F N F_{1}

és az

O F H F_{2}

négyszögek húrnégyszögek. Ezekben a húrnégyszögekben viszont

N O F ∢ = N F_{1} F ∢ = α

, illetve

H O F ∢ = H F_{2} F ∢ = α

. Tehát az

N O F

és a

H O F

háromszögek megegyeznek egy oldalban (

O F

) és a rajta lévő két szögben (

90^{\circ}

, illetve

α

), ezért a két háromszög egybevágó, azaz

N F = F H

.
Ebben a bizonyításban kihasználtuk, hogy

O

és

F

különböző pontok. Ha

O \equiv F

(2. ábra), akkor az

O

-ra vonatkozó szimmetria miatt nyilvánvaló, hogy

N F = F H

.
Tehát az

R S

egyenes mindenképpen felezi az

F B

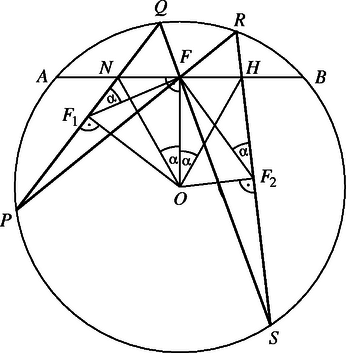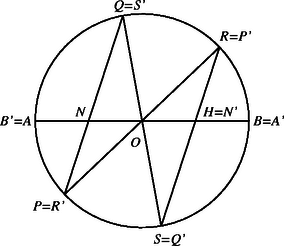szakaszt.

Szépszó Gabriella (Bonyhád, Petőfi S. Evang. Gimn., II. o.t.) dolgozata alapján

Megjegyzés. Teljesen hasonló módon látható be, hogy ha

N

nem negyedelőpont, hanem tetszőleges pont az

A F

szakaszon, akkor is teljesül, hogy

N F = F H

. Ezt a tételt ‐ az 1. ábrán látható, hogy miért ‐, pillangó tételnek nevezik.