Feladat:	Gy.2962	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bérczi Gergely ,  Czirok Levente ,  Fejős Ibolya ,  Formanek Csaba ,  Jenei Piroska ,  Krizsán Árpád ,  Meggyesi Csaba ,  Pintér Dömötör ,  Varga Eszter ,  Zsíros András
Füzet:	1995/október, 413 - 414. oldal		PDF  |  MathML
Témakör(ök):	Háromszög-egyenlőtlenség alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1995/január: Gy.2962

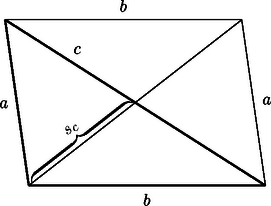
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Tükrözzük a háromszöget a $c$ oldal felezőpontjára. Így egy olyan paralelogrammát kapunk, amelynek szemközti oldalai $a$ és $b$, egyik átlója $c$, a másik átlója pedig $2s_c$ hosszúságú, ahol $s_c$ az eredeti háromszög $c$-hez tartozó súlyvonalának a hossza (1. ábra). Tudjuk, hogy a paralelogramma oldalainak négyzetösszege egyenlő az átlók négyzetösszegével, ezért $\begin{array}{c}{\displaystyle 2\left(a^2+b^2\right)=c^2+4s_c^2\mathrm{.}}\end{array}$   1. ábra   Vagyis $2\left(a^2+b^2\right)-c^2=4s_c^2>0$, amiből rögtön adódik a bizonyítandó állítás. Mivel $s_c^2$ tetszőlegesen kicsi lehet, azért a fenti összefüggésből az is következik, hogy nem írhatunk 2-nél kisebb szorzót.  Krizsán Árpán (Dombóvár, Illyés Gy. Gimn., II. o.t.) dolgozata alapján   II. megoldás. A háromszög-egyenlőtlenségből következik, hogy ${\left(a+b\right)}^2>c^2$. Ugyanakkor nyilvánvalóan ${\left(a-b\right)}^2\ge 0$. 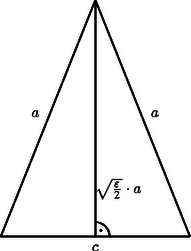E két egyenlőtlenséget összeadva éppen a bizonyítandó állítást kapjuk: $\begin{array}{c}{\displaystyle {\left(a+b\right)}^2+{\left(a-b\right)}^2=2\left(a^2+b^2\right)>c^2\mathrm{.}}\end{array}$   2. ábra   Megmutatjuk, hogy tetszőleges $0<\epsilon <2$ számhoz van olyan háromszög, amelynek oldalaira $\begin{array}{c}{\displaystyle \left(2-\epsilon \right)\left(a^2+b^2\right)=c^2\mathrm{,}}\end{array}$ azaz az eredeti egyenlőtlenségben a bal oldalon nem írhatunk 2-nél kisebb szorzót. Tekintsük azt az egyenlő szárú háromszöget, amelyben $a=b$, az alaphoz tartozó magasság pedig  $m=\sqrt[]{\frac{\epsilon }{2}}a$ (2. ábra). Ekkor Pitagorasz tétele szerint ${\left(\frac{c}{2}\right)}^2=a^2-m^2=a^2\left(1-\frac{\epsilon }{2}\right)$, vagyis $c^2=\left(2-\epsilon \right)\cdot 2a^2=\left(2-\epsilon \right)\left(a^2+b^2\right)$.