Feladat:	F.3097	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Braun Gábor ,  Csávás Csaba ,  Elek Péter ,  Gyukics Mihály ,  Horváth Gábor ,  Makai Márton ,  Péter Zsolt ,  Sánta Zsuzsa ,  Szobonya László ,  Terpai Tamás ,  Vörös Zoltán
Füzet:	1996/április, 221 - 222. oldal		PDF  |  MathML
Témakör(ök):	Számtani-mértani egyenlőtlenségek, Húrnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1995/december: F.3097

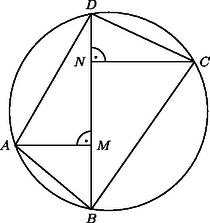
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A feladat megoldásához szükségünk lesz egy egyszerű ismeretre. A szokásos jelölésekkel a háromszög területe kétféleképpen fölírva: $\frac{abc}{4R}=\frac{c\cdot m_c}{2}$. Ebből $\begin{array}{c}{\displaystyle a\cdot b=2R{m}_c\mathrm{.}}\end{array}$ (1) Az ábra jelöléseit használva alkalmazzuk (1)-et az $ABD$ és $BCD$ háromszögekre: $\begin{array}{c}{\displaystyle AB\cdot DA=2AM\mathrm{,}\text{illetve}BC\cdot CD=2CN\mathrm{.}}\end{array}$ (2) A feladat feltétele és (2) szerint $AB\cdot BC\cdot CD\cdot DA=2AM\cdot 2CN\ge 4$, amiből $\begin{array}{c}{\displaystyle AM\cdot CN\ge \mathrm{1,}CN\ge \frac{1}{AM}\mathrm{.}}\end{array}$ (3) Mivel a kör átmérője $2$, $AM+CN\le 2$, amiből (3) alapján $AM+\frac{1}{AM}\le 2$. Ismeretes, hogy pozitív szám és reciprokának összege legalább $2$, ezért előbbi eredményünkkel $2\le AM+\frac{1}{AM}\le 2$. Ez akkor és csak akkor lehetséges, ha $AM=\frac{1}{AM}=1$. Ebből az is látható, hogy $CN=1$, és $M$, $N$ egybeesik a kör középpontjával. De akkor $AC$ és $BD$ a kör két egymásra merőleges átmérője, amiből következik, hogy $ABCD$ négyzet.  Horváth Gábor (Debrecen, Fazekas M. Gimn., I. o.t.)   II. megoldás. A négyszög oldalai nemnegatív számok, ezért a számtani és mértani közép közötti egyenlőtlenség szerint: $\sqrt[]{\left(AB\cdot CD\right)\left(BC\cdot DA\right)}\le \frac{AB\cdot CD+BC\cdot DA}{2}$. A Ptolemaiosz-tétel alapján: $AB\cdot CD+BC\cdot DA=AC\cdot BD$. Két megállapításunk és a feladat feltétele szerint: $4\le {\left(\sqrt[]{\left(ab\cdot cd\right)\left(BC\cdot DA\right)}\right)}^2\le {\left(\frac{AB\cdot CD+BC\cdot DA}{2}\right)}^2={\left(\frac{AC\cdot BD}{2}\right)}^2\le {\left(\frac{2\cdot 2}{2}\right)}^2=4$, ahol felhasználtuk azt is, hogy $AC\le 2$ és $BC\le 2$. A fölírt relációk csak úgy teljesülhetnek, ha mindenütt egyenlőség érvényes, vagyis $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle AC}& {\displaystyle =BD=2}\hfill & \hfill {\displaystyle \left(1\right)}\\ \multicolumn{3}{c}{\text{<br>és}}\\ \hfill {\displaystyle AB\cdot CD}& {\displaystyle =BC\cdot DA\mathrm{.}}\hfill & \hfill {\displaystyle \left(2\right)}\end{array}}}\end{array}$ (1)-ből következik, hogy $AC$ és $BD$ átmérők, tehát $ABCD$ legalább téglalap. A téglalapban $AB=CD$ és $BC=DA$, de akkor (2)-ből $A{B}^2=B{C}^2$, azaz $AB=BC$. Ezért ebben a téglalapban a szomszédos oldalak is egyenlők, tehát négyzet. Könnyű látni, hogy $AB=\sqrt[]{2}$ oldallal a megoldás létezik és ekkor a feltételben egyenlőség áll fenn.  Szobonya László (Fazekas M. Főv. Gyak. Gimn., IV. o.t.)   Megjegyzés. Szobonya László megmutatta, hogy ha az egységsugarú körbe írt konvex $n$-szög oldalainak szorzata nagyobb vagy egyenlő, mint ${\left(2\cdot \text{sin}\frac{\pi }{n}\right)}^n$ $\left(n\ge 3\right)$, akkor az $n$-szög szabályos, és a feltételben egyenlőség lesz. Feladatunk ennek az általánosabb problémának $n=4$-re adódó speciális esete.