Kezdőlap


Feladat:	F.3080	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bujdosó Ildikó , Nagy Margit
Füzet:	1996/február, 94 - 95. oldal		PDF \| MathML
Témakör(ök):	Kör geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1995/szeptember: F.3080

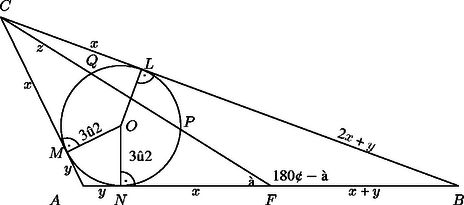
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit. Mivel a $Q$ és $P$ pontok a $C F$ szakaszt három egyenlő részre osztják, a $C$ és $F$ pontoknak a beírt körre vonatkozó hatványa egyenlő. Ezért a $C M$ és $F N$ érintszakaszok egyenlők, ábránkon $x$ nagyságúak. Az $A N = A M = y$ jelöléssel $A F = F B = x + y$ , és így a $B$ -ből húzott érintőszakaszok egyenlősége révén $B L = 2 x + y$ . A $C Q = Q P = P F = z$ jelöléssel, a $C$ -ből húzott érintőszakaszra és szelődarabokra vonatkozó tétel szerint $x^{2} = z \cdot 2 z$ , amiből $z = \frac{x}{\sqrt[]{2}}$ és $C F = \frac{3 x}{\sqrt[]{2}}$ .
Ezután a feladatot úgy fogjuk megoldani, hogy a koszinusztétel és területképletek segítségével kiszámítjuk $x$ -et és $y$ -t. Alkalmazzuk a koszinusztételt az $A F C$ és $B F C$ háromszögekre:

\begin{matrix} \begin{matrix} {(x + y)}^{2} = \frac{9 x^{2}}{2} + {(x + y)}^{2} - 2 \cdot \frac{3 x}{\sqrt[]{2}} (x + y) cos α, \\ {(3 x + y)}^{2} = \frac{9 x^{2}}{2} + {(x + y)}^{2} - 2 \cdot \frac{3 x}{\sqrt[]{2}} (x + y) cos (180^{\circ} - α) . \end{matrix} \end{matrix}

A két egyenletet összeadva:

\begin{matrix} {(x + y)}^{2} + {(3 x + y)}^{2} = 9 x^{2} + 2 {(x + y)}^{2}, ebből x^{2} = 4 x y, \end{matrix}

és mivel

x \neq 0

x = 4 y

. Ezután a háromszög oldalai

A C = 5 y

B C = 13 y

A B = 10 y

, és a félkerület

s = 14 y

. Az

A B C

háromszög területét kétféleképpen fölírva:

\begin{matrix} 3 \cdot \sqrt[]{2} \cdot 14 y = \sqrt[]{14 y \cdot y \cdot 9 y \cdot 4 y}, amiből y = \sqrt[]{7} . \end{matrix}

Az oldalak

A C = 5 \sqrt[]{7}

B C = 13 \sqrt[]{7}

A B = 10 \sqrt[]{7}

Bujdosó Ildikó (Bp., Veres Péter Gimn., IV. o.t.) és

Nagy Margit (Vörösmarty M. Gimn., III. o.t.) dolgozata alapján

Megjegyzés. A közölt megoldásból csak az derül ki, hogy ha létezik a feladat követelményeit kielégítő háromszög, akkor annak oldalai csak

5 \sqrt[]{7}

13 \sqrt[]{7}

10 \sqrt[]{7}

lehetnek. Könnyű számolással meggyőződhetünk azonban arról, hogy e háromszög beírt köre valoban három egyenlő részre vágja a

C F

súlyvonalat.