Feladat:	F.3079	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Bakos Péter ,  Járási István ,  Kopecsni György ,  Kutalik Zoltán ,  Makai Márton ,  Pap Júlia ,  Sánta Zsuzsa ,  Szobonya László
Füzet:	1996/április, 213 - 214. oldal		PDF  |  MathML
Témakör(ök):	Kör geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1995/szeptember: F.3079

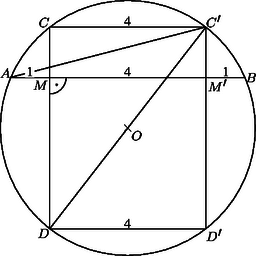
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük a húrok metszéspontját $M$-mel, és legyen $AM=1$ egység. Tükrözzük a $CD$ húrt az $AB$ felező merőlegesére (1. ábra). Nyilván $CDD\text{'}C\text{'}$ egy téglalap, és ezért $DD\text{'}=CC\text{'}=MM\text{'}=4$. Mivel a hosszabbik $AB$ köríven a $D$ pont van, az $AD$ ív fele a $DB$ ívnek. A tükrözés folytán az $AD$ ív és a $BD\text{'}$ ív egyenlő, ezért előbbi megjegyzésünket is figyelembe véve $AD=BD\text{'}=DD\text{'}=4$. Az elmondottakból következik, hogy az $ADC\text{'}C$ négyszögben $AD=CC\text{'}=4$, és ennek a húrnégyszögnek a $DC\text{'}$ oldala a kör egy átmérője. Ezért ez a négyszög szimmetrikus $DC\text{'}$ felező merőlegesére. De akkor az $ADC$ és a $CC\text{'}A$ háromszögek egybevágók, amiért területük egyenlő: $\frac{CD\cdot 1}{2}=\frac{4\cdot CM}{2}$. Ebből következik, hogy $CD=4\cdot CM$, amiből $MD=3\cdot CM$, tehát $CM:MD=1:3$.  Pap Júlia (Debrecen, Fazekas M. Gimn, I. 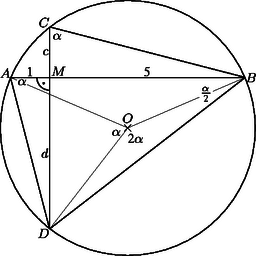o.t.) dolgozata alapján   II. megoldás. Legyen az $AOD\sphericalangle =\alpha$. A második feltétel szerint $BOD\sphericalangle =2\alpha$, és így $AOB\sphericalangle ={360}^{\circ }-3\alpha$ (lásd 2. ábra). A kerületi és középponti szögek összefüggése alapján $ABD\sphericalangle =\frac{\alpha }{2}$, $BCD\sphericalangle =\alpha$, $ADB\sphericalangle ={180}^{\circ }-\frac{3}{2}\alpha$. A húrok merőlegességéből következik, hogy $ABC\sphericalangle =ADC\sphericalangle ={90}^{\circ }-\alpha$. Ezután belátjuk, hogy a $BCD$ háromszög egyenlő szárú. $CDB\sphericalangle ={180}^{\circ }-\frac{3}{2}\alpha -\left({90}^{\circ }-\alpha \right)={90}^{\circ }-\frac{\alpha }{2}$, $CBD\sphericalangle =\frac{\alpha }{2}+\left({90}^{\circ }-\alpha \right)={90}^{\circ }-\frac{\alpha }{2}$, amiből valóban következik, hogy $CB=CD=c+d$. Legyen most is $AM=1$. Az $AMD$ és $CMB$ háromszögek hasonlóságából $\frac{1}{d}=\frac{c}{5}$, amiből $c=\frac{5}{d}$. A $CMB$ háromszögre a Pitagorasz-tételt alkalmazva $c^2+5^2={\left(c+d\right)}^2$, majd fölhasználva, hogy $c=\frac{5}{d}$, $d=\sqrt[]{15}$ adódik. A keresett arány $c:d=\frac{5}{\sqrt[]{15}}:\sqrt[]{15}=1:3$.  Bakos Péter (Eger, Szilágyi E. Gimn., III. o.t.)   Megjegyzés: Többen trigonometriai ismeretek felhasználásával oldották meg a feladatot.