Feladat:	F.3064	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Farkas Péter ,  Ugron Balázs
Füzet:	1995/december, 532 - 533. oldal		PDF  |  MathML
Témakör(ök):	Indirekt bizonyítási mód, Egyenlőtlenségek grafikus megoldása, Abszolútértékes egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1995/április: F.3064

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Az állítást indirekten igazoljuk. Tegyük fel, hogy az állítás hamis. Ekkor az $x$, $y$, $z$ számokra a következő három egyenlőtlenség teljesül: $\begin{array}{c}{\displaystyle |x|<|y-z|;|y|<|z-x|;|z|<|x-y|\mathrm{.}}\end{array}$ Ez a feltétel $x$, $y$, $z$-re szimmetrikus, ezért elég azt az esetet vizsgálni, amikor $x\le y\le z$. Ekkor a jobb oldalon az abszolút érték helyett írhatjuk: $\begin{array}{c}{\displaystyle |x|<z-y;|y|<z-x;|z|<y-x\mathrm{.}}\end{array}$ Adjuk össze az első és a harmadik egyenlőtlenséget: $\begin{array}{c}{\displaystyle |x|+|z|<z-x\mathrm{.}}\end{array}$ Mivel $z-x\le |z|+|x|$, ez ellentmondás.  Ugron Balázs (Veszprém, Lovassy L. Gimn., III. o.t.)   II. megoldás. Grafikusan oldjuk meg a feladatot. Ha $x$, $y$ és $z$ előjelét felcseréljük, a bizonyítandó állítás nem változik. Feltehetjük tehát, hogy $z\ge 0$. 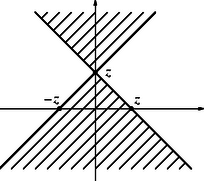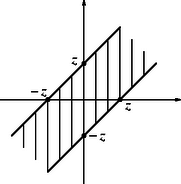Legyen $z$ rögzített, és ábrázoljuk a kétdimenziós $x$, $y$ tengelyű koordináta-rendszerben azokat az