Feladat: F.3057 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bámer Balázs ,  Csiki Tibor Zoltán ,  Dombi Gergely ,  Elek Péter ,  Erdélyi László ,  Farkas Illés ,  Frenkel Péter ,  Hegedűs Viktor ,  Katona János ,  Lolbert Tamás ,  Nagy Katalin ,  Pap Gyula ,  Perényi Márton ,  Radnóti Gergely ,  Rozmán András ,  Sánta Zsuzsa ,  Séllei Béla ,  Terpai Tamás ,  Tóth Gábor Zsolt ,  Ugron Balázs ,  Valkó Benedek ,  Véber Miklós 
Füzet: 1996/február, 88 - 89. oldal  PDF  |  MathML 
Témakör(ök): Gömb és részei, Feladat
Hivatkozás(ok):Feladatok: 1995/február: F.3057

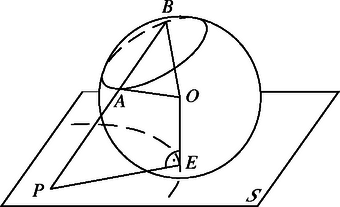
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy a négy pont vagy egy körre, vagy egy egyenesre illeszkedik. Az AB és CD szakaszoknak mindenképpen van közös pontja, egyébként lenne olyan S sík, amelyik a szakaszokat elválasztja. Ekkor pedig az AB és CD szakaszokra illeszthető egy-egy olyan gömb, amelyik az S síkot érinti, s ezért nem metszhetik egymást. Egy ilyen, az A, B pontokon átmenő gömb O középpontját a következőképpen szerkeszthetjük meg. Az AB egyenes közös pontja az S síkkal legyen P. A P körüli r=PA⋅PB sugarú, S-ben lévő kör egy E pontjában az S-re merőleges egyenesnek és AB felező merőleges síkjának közös pontja a keresett O pont (1. ábra). Ha AB párhuzamos S-sel, és AB felezőpontjának S-re eső vetülete F, akkor könnyen szerkeszthető pl. egy A és B-n átmenő S-et F-ben érintő gömb. Hasonlóan kaphatunk a C és D pontokra illeszkedő, az S síkot érintő gömböt.
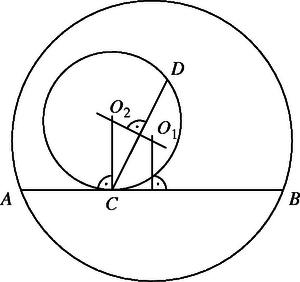
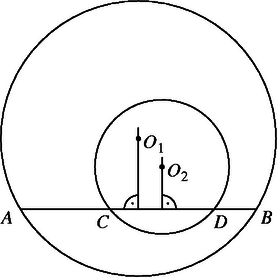
Az A, B, C és D pontok konvex burka nem lehet háromszög vagy az AB, illetve CD valamelyike, mert ezekben az esetekben az A, B illetve C, D pontpárok egyikére illeszkedő gömb tartalmazhatja a másik pontpárra illeszkedő gömböt (2. és 3. ábra).
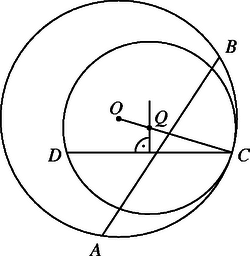
Az eddigiekben megállapítottuk, hogy ha a négy pont egy egyenesen van, akkor A, B elválasztja C, D-t, ha pedig nincs egy egyenesen, akkor az AB és CD szakaszok egy belső pontjukban metszik egymást. Bebizonyítjuk, hogy az utóbbi esetben a négy pont húrnégyszöget alkot. Tegyük fel, hogy a D pont nincs rajta az ABC háromszög köré írt O középpontú körön. Ez esetben a CD szakasz felezőmerőlegesének és az OC egyenesnek a Q közös pontja körüli QC sugarú gömb nem metszi (hanem érinti) az O közepű OA sugarú gömböt, ami ellentmond a feltételnek (4. ábra).
Összefoglalva megállapíthatjuk, hogy az A, B, C, D pontnégyes csak akkor rendelkezik a feladatbeli tulajdonságokkal, ha egy körön, vagy egy egyenesen van, mégpedig úgy, hogy az A, B pontpár elválasztja a C, D pontpárt.
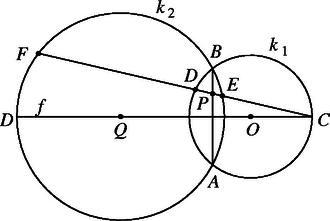
Bebizonyítható, hogy a most kimondott feltételek elegendőek. Ha a pontnégyes egy egyenesen van, akkor a feladatbeli feltételek teljesülése triviális. Az is nyilvánvaló, hogy az A, B és C, D pontpárok egyikére illeszkedő sík metszi a másik pontpárra illeszkedő síkot vagy gömböt. Megmutatjuk, hogy ha a négy pont egy körön van és A, B elválasztja C, D-t, akkor minden, az A, B pontokon átmenő gömb metsz minden, a C, D pontokon átmenő (az előbbiektől különböző) gömböt. Nézzük ehhez az 5. ábrát. Elég belátnunk, hogy az AB szakasz f felezőmerőlegesének bármely O-tól különböző Q pontja körüli r=QA sugarú körlemez a C, D pontok közül pontosan az egyiket tartalmazza; ekkor ugyanis az A, B pontokon átmenő gömb metszi a C, D pontokon átmenő bármelyik gömböt. Az AB és CD metszéspontja legyen P, ez a k1 és k2 körök mindkettejének belső pontja. Legyenek a CD egyenes és k2 közös pontjai E és F. Ekkor a P pont k1-re, illetve k2-re vonatkozó hatványa:

PA⋅PB=PC⋅PD=PE⋅PF.(1)
Mivel P elválasztja mind a C, D mind az E, F pontokat, feltehetjük, hogy E a PC félegyenesen, és így F a PD félegyenesen van. Ha most PC>PE, akkor (1) szerint PD<PF, tehát C a k2 kör külső, D pedig belső pontja. Hasonló a helyzet a PC<PE esetben (PC=PE nem lehetséges, mert akkor k1≡k2, azaz O≡Q lenne).
Tehát egy pontnégyes akkor és csak akkor rendelkezik a feladatban megfogalmazott tulajdonságokkal, ha a négy pont egy körön, vagy egy egyenesen van, és az A, B pontpár elválasztja a C, D pontpárt.