Kezdőlap


Feladat:	F.3051	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Farkas Illés , Farkas Péter , Katona János , Kováts Antal , Varga Tamás , Vörös Zoltán
Füzet:	1995/november, 485. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Feladat
Hivatkozás(ok):	Feladatok: 1995/január: F.3051

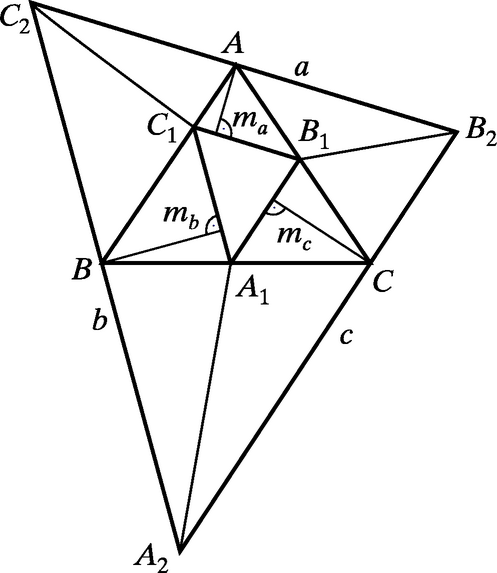
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit, ahol $m_{c}$ az $A_{1} B_{1}$ és $A_{2} B_{2}$ egyenesek távolsága; hasonló szerepűek az $m_{b}$ és $m_{a}$ szakaszok. Az $A B C ▵$ területe legyen $t$ , az $A_{2} B_{2} C_{2} ▵$ oldalai pedig $a$ , $b$ , $c$ . Az oldalak párhuzamossága miatt az $A_{1} B_{1} C_{1}$ és $A_{2} B_{2} C_{2}$ háromszögek hasonlók. Ha a hasonlóság aránya $k$ , akkor $\frac{t_{1}}{t_{2}} = k^{2}$ , azaz $\sqrt[]{\frac{t_{1}}{t_{2}}} = k$ .

Számoljuk ki először az

A_{2} B_{2} C_{2} ▵

területét az ábrán látható 3 trapéz és az

A_{1} B_{1} C_{1} ▵

területének összegeként:

\begin{matrix} \begin{matrix} t_{2} & = \frac{a + k a}{2} m_{a} + \frac{b + k b}{2} m_{b} + \frac{c + k c}{2} m_{c} + t_{1} = \\ = (1 + k) (\frac{a m_{a}}{2} + \frac{b m_{b}}{2} + \frac{c m_{c}}{2}) + k^{2} t_{2} . \end{matrix} \end{matrix}

Ebből

\begin{matrix} t_{2} (1 - k^{2}) = (1 + k) (\frac{a m_{a}}{2} + \frac{b m_{b}}{2} + \frac{c m_{b}}{2}), \end{matrix}

és így

\begin{matrix} t_{2} (1 - k) = \frac{a m_{a}}{2} + \frac{b m_{b}}{2} + \frac{c m_{c}}{2} . \end{matrix}

(1)

Hasonlóan fölírhatjuk az

A B C ▵

területét:

\begin{matrix} t = \frac{k \cdot a}{2} \cdot m_{a} + \frac{k \cdot b}{2} \cdot m_{b} + \frac{k \cdot c}{2} \cdot m_{c} + t_{1}, \end{matrix}

amiből

\begin{matrix} \frac{t - k^{2} \cdot t_{2}}{k} = \frac{a \cdot m_{a}}{2} + \frac{b \cdot m_{b}}{2} + \frac{c \cdot m_{c}}{2} . \end{matrix}

(2)

Mivel (1) és (2) jobb oldala azonos,

t_{2} (1 - k) = \frac{t}{k} - k \cdot t_{2}

, és így

t = k \cdot t_{2}

. Mivel

k = \sqrt[]{\frac{t_{1}}{t_{2}}}

t = \sqrt[]{\frac{t_{1}}{t_{2}}} \cdot t_{2} = \sqrt[]{t_{1} \cdot t_{2}}

. Tehát az

A B C ▵

területe a másik két háromszög területének mértani közepe.

Kováts Antal (Bp., ELTE Radnóti M. Gyak. Gimn., IV. o.t.) és

Varga Tamás (Szigetvár, Zrínyi M. Gimn., III. o.t.)