Feladat:	F.3049	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bámer Balázs ,  Braun Gábor ,  Elek Péter ,  Fejes Tóth Péter ,  Hegedűs Viktor ,  Kocsis Zoltán ,  Lovász Zoltán ,  Majlender Péter ,  Makai Márton ,  Puskás Zsolt ,  Tóth Gábor Zsolt ,  Visontai Mirkó ,  Vörös Zoltán ,  Zaupper Bence
Füzet:	1995/november, 482 - 483. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek nevezetes tételei, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1995/január: F.3049

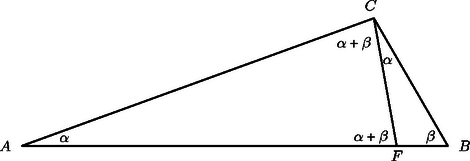
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A feltételből azonnal következik, hogy $\gamma =2\alpha +\beta$. Ebből pedig látjuk, hogy $\gamma >\beta$, és akkor $c>b$. Ennek megfelelően készült az ábra, amelynek $\gamma$ szögét a $CF$ egyenessel felosztottuk $\alpha +\beta$ és $\alpha$ nagyságú szögekre. A feltétel alapján $AFC\sphericalangle =\alpha +\beta$, hiszen a $CBF▵$ külső szöge. Ezért az $AFC▵$ egyenlő szárú, amiért $AF=b$ és $FB=c-b$. Könnyen látható, hogy $ABC▵\sim CBF▵$, ugyanis a két háromszög szögei páronként egyenlők. Tehát a megfelelő oldalak aránya is megegyezik: $\frac{c-b}{a}=\frac{a}{c}$, amiből $a^2+bc-c^2=0$, amint azt bizonyítani kellett.      Fejes Tóth Péter (Bp., Árpád Gimn., III. o.t.) és    Lovász Zoltán (Bonyhád, Perczel Mór Közg Szki., IV. o.t.)   II. megoldás. A szinusztétel alapján $a=\frac{b\cdot \text{sin}\alpha }{\text{sin}\beta }$, illetve $c=\frac{b\cdot \text{sin}\left(2\alpha +\beta \right)}{\text{sin}\beta }$. Az $a$ és $c$ ezen kifejezéseivel: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a^2+bc-c^2}& {\displaystyle =b^2\cdot \frac{\text{sin}{}^2\alpha }{\text{sin}{}^2\beta }+b^2\cdot \frac{\text{sin}\left(2\alpha +\beta \right)}{\text{sin}\beta }-b^2\cdot \frac{\text{sin}{}^2\left(2\alpha +\beta \right)}{\text{sin}{}^2\beta }=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{b^2}{\text{sin}{}^2\beta }\cdot \left[\text{sin}{}^2\alpha +\text{sin}\beta \cdot \text{sin}\left(2\alpha +\beta \right)-\text{sin}{}^2\left(2\alpha +\beta \right)\right]\mathrm{.}}\hfill \end{array}}}\end{array}$ Ezek után azt kell megmutatnunk, hogy a szögletes zárójelben lévő kifejezés értéke zérus. Ezt ‐ ismert összefüggéseket és a feltételt fölhasználva ‐ így láthatjuk be: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \left[\text{sin}\alpha +\text{sin}\left(2\alpha +\beta \right)\right]\left[\text{sin}\alpha -\text{sin}\left(2\alpha +\beta \right)\right]+\text{sin}\beta \cdot \text{sin}\left(2\alpha +\beta \right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{sin}\beta \cdot \text{sin}\left(2\alpha +\beta \right)+2\cdot \text{sin}\frac{3\alpha +\beta }{2}\cdot \text{cos}\frac{\alpha +\beta }{2}\cdot 2\text{cos}\frac{3\alpha +\beta }{2}\cdot \text{sin}\frac{-\alpha -\beta }{2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{sin}\beta \cdot \text{sin}\left(2\alpha +\beta \right)+\text{sin}\left(3\alpha +\beta \right)\cdot \left[-\text{sin}\left(\alpha +\beta \right)\right]=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{sin}\beta \cdot \text{sin}\left[{180}^{\circ }-\left(\alpha +\beta \right)\right]+\text{sin}\left({180}^{\circ }-\beta \right)\cdot \left[-\text{sin}\left(\alpha +\beta \right)\right]=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{sin}\beta \left[\text{sin}\left(\alpha +\beta \right)-\text{sin}\left(\alpha +\beta \right)\right]=\mathrm{0,}}\hfill \end{array}}}\end{array}$ ami a feladat állítását igazolja.  Hegedűs Viktor (Paks, Vak Bottyán Gimn., IV. o.t.)   Megjegyzések. 1. Hegedűs Viktor megmutatta, hogy a feladat állítása megfordítható. Ezt az I. megoldás alapján könnyen beláthatjuk. 2. A $\gamma =2\alpha +\beta$ összefüggésből $2\gamma =4\alpha +2\beta =\alpha +{180}^{\circ }$, amiből következik, hogy a háromszög tompaszögű.