Kezdőlap


Feladat:	C.415	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bálint Olivér , Gáspár Merse Előd , Hajdufi Péter , Méder Áron , Sarlós Ferenc , Szita István
Füzet:	1996/szeptember, 345 - 347. oldal		PDF \| MathML
Témakör(ök):	Koordináta-geometria, Deltoidok, C gyakorlat
Hivatkozás(ok):	Feladatok: 1995/december: C.415

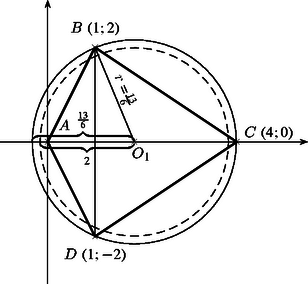
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Könnyen beláthatjuk, hogy a deltoid köré nem írható kör, azaz nem húrnégyszög. Ugyanis, ha húrnégyszög lenne, akkor a szimmetria miatt ez most azt jelentené, hogy a $B$ és $D$ csúcsánál derékszög van. Ez azonban nem igaz. Az $A B$ egyenes iránytangense (könnyen leolvasható a koordinátáiból) $2$ , míg a $B C$ egyenesé $- 2 / 3$ , azaz a két egyenes nem merőleges egymásra. Nincs tehát olyan kör, amely mind a $4$ pontot a belsejében tartalmazza (vagy a $4$ pont a körön kívül fekszik) és azoktól egyenlő távolságra van. Ha ugyanis ilyen kör létezne, akkor a középpontból kicsinyítve, (vagy nagyítva) a kör átmenne a deltoidnak mind a $4$ csúcsán.
Így csak az lehetséges, hogy

(a) $3$ pont az egyik (a körön belüli) és $1$ pont a másik a (körön kívüli) síkrészben van,

vagy

(b) $2$ pont a körön belül, $2$ a körön kívül fekszik.
Az a) esetben is $3$ lehetőségünk van,

1. ha az $A$ pont van kívül,

2. ha a $B$ pont van kívül (a szimmetria miatt ez ugyanaz, mintha $D$ pont lenne kívül),

3. ha a $C$ pont van kívül.
Az 1. esetben először írjuk fel a $B$ , $C$ , $D$ pontokon átmenő kör egyenletét. A kör középpontjának koordinátái $O_{1} (\frac{11}{6}; 0)$ és sugara $r = \frac{13}{6}$ . Látható, hogy az $A$ pont a körön belül van, hiszen $O_{1} A = \frac{11}{6} < \frac{13}{6}$ . Ezt a kört kell zsugorítani az $O_{1}$ pontból úgy, hogy egyenlő távolságra legyen mind a 4 ponttól. Ez akkor teljesül, ha

\begin{matrix} r_{1} = \frac{\frac{11}{6} + \frac{13}{6}}{2} = 2 \end{matrix}

egységnek választjuk a kör sugarát.
A 2. és 3. esetben a számítás hasonlóan elvégezhető, itt csak az eredményeket közöljük.
A 2. esetben a kör

O_{2}

középpontjának koordinátái

(2; - \frac{1}{4})

, sugara

r_{2} = \frac{\sqrt[]{65} + \sqrt[]{97}}{8} \approx 2,23889

.
A 3. esetben

r_{3} = 2

. (

O_{3}

koordinátái

(\frac{5}{2}; 0)

)
b) Végül marad az a 2 eset, amikor a kör szétválasztja a pontokat.
Legyenek a szétválasztott pontok

A B

és

C D

. Írjuk fel mindkét szakasz felezőmerőlegesének egyenletét. Ezek metszéspontja egyenlő távolságra lesz

A

-tól és

B

-től, illetve

C

-től és

D

-től. Számítsuk ki ezeket a távolságokat.
Az

A B

szakasz felezőpontjának koordinátái

(\frac{1}{2}; 1)

, az

A B

egyenes iránytangense

2

f_{1}

felező merőlegesének egyenlete

y - 1 = - \frac{1}{2} (x - \frac{1}{2})

; a

C D

szakasz felezőpontjának koordinátái

(\frac{5}{2}; - 1)

, a

C D

egyenes iránytangense

\frac{2}{3}

f_{2}

felező merőlegesének egyenlete

y + 1 = - \frac{3}{2} (x - \frac{5}{2})

f_{1}

és

f_{2}

metszéspontjának koordinátái

O_{4} (\frac{3}{2}; \frac{1}{2})

\begin{matrix} \bar{O_{4} A} = \bar{O_{4} B} = \sqrt[]{{(\frac{3}{2})}^{2} + {(\frac{1}{2})}^{2}} = \frac{\sqrt[]{10}}{2}, O_{4} C = O_{4} D = \sqrt[]{{(\frac{5}{2})}^{2} + {(\frac{1}{2})}^{2}} = \frac{\sqrt[]{26}}{2} . \end{matrix}

Ha tehát

O_{4}

körül egy olyan kört rajzolunk, amelynek sugara

r_{4} = \frac{\frac{\sqrt[]{10}}{2} + \frac{\sqrt[]{26}}{2}}{2} \approx 2,065

, ez mind a

4

ponttól egyenlő távolságra lesz, mégpedig

A

B

a körön belül

C

D

a körön kívül. (a tengelyes szimmetria miatt az

A

D

és

B

C

szétválasztása ugyanezt az eredményt adja).
Végül legyen

B

C

és

A

D

a szétválasztott pontpár, és ugyanígy írjuk fel a szakaszfelező merőleges egyenesek metszéspontját. Az eredmény

\begin{matrix} O_{5} (2; 0) és r_{5} = \frac{2 + \sqrt[]{5}}{2} \approx 2,118. \end{matrix}

Láthatjuk, hogy a legnagyobb sugár az

r_{2} = 2,23889

; ezt akkor kaptuk, amikor a

B

pont a körön kívül,

A

C

D

pedig azon belül helyezkedett el.

Méder Áron (Budapest, Táncsics M. Gimn., II. o.t.)