Kezdőlap


Feladat:	C.399	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Egyed Gábor , Hajdú Viktória , Hegedűs Dalma , Nagy Andrea , Némedi Richárd
Füzet:	1996/január, 10 - 11. oldal		PDF \| MathML
Témakör(ök):	Trapézok, C gyakorlat
Hivatkozás(ok):	Feladatok: 1995/május: C.399

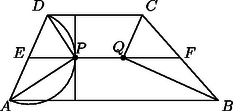
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először azt az esetet vizsgáljuk, amikor $A B + D C > D A + C B$ . Belátjuk, hogy ekkor a $P Q$ szakasz a trapéz középvonalának része.
Mivel $P$ az $A$ és $D$ csúcsból húzott belső szögfelezők metszéspontja, így egyenlő távolságra van az $A D$ , $A B$ , $D C$ oldalaktól, vagyis felezi az $A B$ és $D C$ oldalak távolságát. Ugyanez mondható el a $Q$ pontról is, amelyik a $C$ és $B$ csúcsban lévő szögek szögfelezőinek metszéspontja. $P$ és $Q$ tehát pontja a középvonalnak.
Könnyen igazolható az is, hogy az $A D P$ háromszög $P$ -nél lévő szöge, illetve a $B C Q$ háromszög $Q$ -nál lévő szöge derékszög. Tudjuk, hogy a trapéz egy szárán fekvő szögeinek összege $180^{\circ}$ , a szögfelezők ezeket a szögeket felezik, amiből következik, hogy $D A P ∢ + A D P ∢ = 90^{\circ}$ , vagyis $P$ -nél derékszög van, hasonlóképpen a $Q$ -nál lévő szög is derékszög.
Húzzuk meg a trapéz középvonalát; ez $A D$ -t $E$ -ben, $C B$ -t $F$ -ben metszi. Az $A D$ szakasz fölé rajzolt Thalész-kör középpontja $E$ és így

\begin{matrix} A E = E D = E P = \frac{A D}{2}, \end{matrix}

hasonlóan

\begin{matrix} B F = F C = F Q = \frac{B C}{2} . \end{matrix}

Ezeket felhasználva

\begin{matrix} P Q = E F - F Q - E P = \frac{A B + D C}{2} - \frac{B C}{2} - \frac{A D}{2} = \frac{A B - B C + C D - A D}{2}, \end{matrix}

s mivel feltettük hogy

\begin{matrix} A B + D C > B C + A D, \end{matrix}

így

\begin{matrix} E F = \frac{A B + D C}{2} > \frac{B C}{2} + \frac{A D}{2} = F Q + P E, \end{matrix}

a különbség pozitív.
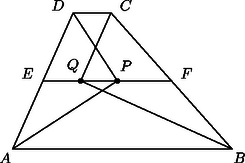
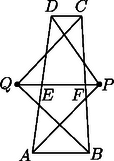
Az állítás akkor is igaz, ha

A B + D C < B C + D A

, mint az a 2. és 3. ábrán is látható. A bizonyítás is teljesen hasonló, csak mivel most az

E F - F Q - E P

különbség nem pozitív, a különbség abszolút értékét kall venni; ezért szerepelt az abszolút érték jel a feladat állításában.

Némedi Richárd, (Budapest ELTE Apáczai Cs. János Gimn., IV. o. t.)