Feladat:	C.395	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bálint Olivér ,  Baranyai Szabolcs ,  Béczi Rita ,  Borbély Eszter ,  Egyed Gábor ,  Fülöp Levente ,  Geisz Gábor ,  Gueth Krisztián ,  Hajdú Viktória ,  Harrach Nóra Viola ,  Hegedűs Éva ,  Heringer Dávid ,  Jáger Márta ,  Kálmán Krisztina ,  Kolláth Kornél ,  Kovács Emőke ,  Kovács Károly ,  Lukács Erika ,  Majlender Péter ,  Márkus Erika ,  Márton Izabella ,  Méder Áron ,  Nagy Andrea ,  Nagy Margit ,  Nagy Zoltán Zsolt ,  Németh László ,  Papp Ágnes ,  Papp András ,  Pastyik Noémi ,  Rácz Enikő ,  Sarlós Ferenc ,  Sasvári Valéria ,  Szabadszállási Tibor ,  Szedmák Diána ,  Szita István ,  Zsók Gabriella
Füzet:	1996/január, 9 - 10. oldal		PDF  |  MathML
Témakör(ök):	Trigonometriai azonosságok, Pitagorasz-tétel alkalmazásai, C gyakorlat
Hivatkozás(ok):	Feladatok: 1995/április: C.395

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Rajzoljunk egy derékszögű háromszöget, amelynek befogói 8 és 15 egység hosszúak, a 8 egységgel szemben levő hegyesszöge $\alpha$, másik hegyesszöge $\beta$, az átfogó $AB=\sqrt[]{8^2+{15}^2}=17$. Forgassuk le az $AB$ átfogót a $CA$ félegyenesre. Az $ABD$ egyenlő szárú háromszögben $AD=17$,  $BDA\sphericalangle =ABD\sphericalangle =\frac{\alpha }{2}$. Az $ABC$ háromszögből $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =\frac{8}{15}$, hiszen $\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{8}{15}=\alpha$. A $BCD$ háromszögből $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(\frac{\alpha }{2}+\beta \right)=\frac{32}{8}=\mathrm{4,}\text{innen}\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}4=\frac{\alpha }{2}+\beta \mathrm{.}}\end{array}$ Mivel $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \beta =\frac{\pi }{2}-\alpha \mathrm{,}}\\ \hfill {\displaystyle \text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}4=\frac{\alpha }{2}+\beta =\frac{\alpha }{2}+\frac{\pi }{2}-\alpha =\frac{\pi }{2}-\frac{\alpha }{2}\mathrm{.}}\end{array}}}\end{array}$ Azaz $\begin{array}{c}{\displaystyle 2\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}4=\pi -\alpha =\pi -\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{8}{15}\mathrm{.}}\end{array}$ Ezt behelyettesítve a hányados értéke: $\begin{array}{c}{\displaystyle \frac{\pi -\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{8}{15}}{\pi -\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{8}{15}}=1.}\end{array}$  Egyed Gábor, (Szombathely, Orlay F. Károly Szakközépisk., III. o. t.)   II. megoldás. Legyen $\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{8}{15}=\alpha$, $\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}4=\beta$. Ekkor $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =\frac{8}{15}$ és $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta =4$. Írjuk fel $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}2\beta$-ra az ismert összefüggést: 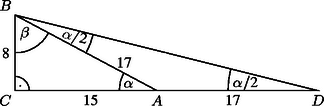$\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}2\beta =\frac{2\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta }{1-\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\beta }=\frac{8}{1-4^2}=-\frac{8}{15}=-\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \mathrm{,}}\end{array}$ mivel  $-\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(\pi -\alpha \right)$,  $2\beta =\pi -\alpha$  ($0<\alpha$, $\beta <\frac{\pi }{2}$). Behelyettesítve $\alpha$ és $\beta$ értékét $\begin{array}{c}{\displaystyle 2\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}4=2\beta =\pi -\alpha =\pi -\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{8}{15}\mathrm{,}}\end{array}$ tehát a hányados értéke 1.   Megjegyzés. A megoldásban felhasználtuk, hogy $\pi -\alpha$ és $2\beta$ a $\left(\mathrm{0,}\pi \right)$ intervallumba esik, mert különben nem lenne igaz az, hogy ha $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(\pi -\alpha \right)=\text{<span style="font-weight: normal;font-style: normal;">tg</span>}2\beta$-val, akkor $\pi -\alpha =2\beta$.