Kezdőlap


Feladat:	C.383	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bakonyi Zoltán , Csibi Attila , Egyed Gábor , Fazekas Péter , Hegedűs Dalma , Majlender Péter , Zaupper Bence
Füzet:	1995/október, 405 - 407. oldal		PDF \| MathML
Témakör(ök):	Műveletek helyvektorok koordinátáival, Két pont távolsága, szakasz hosszúsága, Kör egyenlete, Másodfokú (és arra visszavezethető) egyenletek, Húrnégyszögek, C gyakorlat
Hivatkozás(ok):	Feladatok: 1995/január: C.383

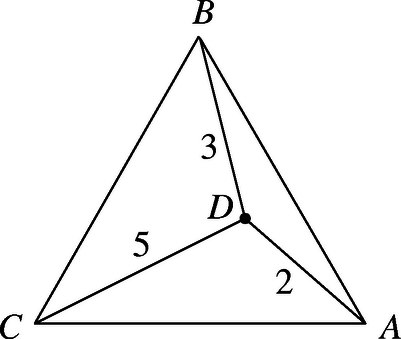
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először vizsgáljuk meg, mit mondhatunk a $D$ pont helyzetéről. Tegyük fel, hogy a $D$ pont a háromszög belsejében van, és legyen pl. $A$ -tól 2, $B$ -től 3, $C$ -től 5 egységnyire. Mivel a háromszög szabályos, egyik csúcsának sincs kitüntetett szerepe. A $D$ pont az 1. ábrán a $C$ körüli 5 egység, $B$ körüli 3 egység, $A$ körüli 2 egység sugarú körök közös pontja. Mivel $C D = 5$ , $D$ csak úgy lehet a háromszög belsejében, ha $A C$ , azaz a háromszög oldala hosszabb 5 egységnél, de akkor az $A$ és $B$ körüli 2 és 3 egység sugarú köröknek nem lehet metszéspontjuk. $D$ tehát nem lehet belső pont. Hasonlóan látható be, hogy $D$ nem lehet az $A C$ , $B C$ oldalakon sem.
Ha $D$ pl. az $A B$ szakaszon lenne, akkor az $A$ és $B$ körüli körök metszéspontja lenne, ami azt jelentené, hogy $A B = 5$ egység, de akkor $D$ nem lehetne $C$ -től 5 egységnyire. $D$ tehát csak a háromszögön kívül helyezkedhet el.
A feladat további részére három különböző megoldást mutatunk be.

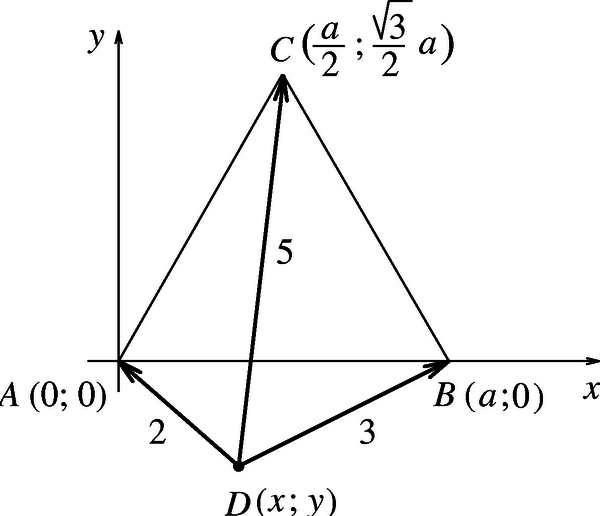
I. megoldás. Helyezzük el a szabályos háromszöget egy derékszögű koordináta-rendszerbe úgy, hogy az

A

csúcsa az origóba, az

A B

oldalegyenese az

x

tengelyre essék. A háromszög oldalának hosszát jelölje

a

, ekkor a csúcsok koordinátái

A (0; 0)

B (a; 0)

C (\frac{a}{2}; \frac{\sqrt[]{3}}{2} a)

. Legyenek a

D

pont koordinátái

(x; y)

, és

| \vec{D A} | = 2

| \vec{D B} | = 3

| \vec{D C} | = 5

, amelyeket koordinátákra felírva az

\begin{matrix} \begin{matrix} x^{2} + y^{2} & = 4, & (1) \\ {(x - a)}^{2} + y^{2} & = 9, & (2) \\ {(x - \frac{a}{2})}^{2} + {(y - \frac{\sqrt[]{3}}{2} a)}^{2} & = 25. & (3) \end{matrix} \end{matrix}

egyenletrendszert kapjuk.
Elvégezzük a négyzetreemeléseket és összevonásokat:

\begin{matrix} \begin{matrix} x^{2} - 2 a x + a^{2} + y^{2} & = 9, & (2') \\ x^{2} - a x + y^{2} - \sqrt[]{3} a y + a^{2} & = 25. & (3') \end{matrix} \end{matrix}

(1)

-ből

x^{2} + y^{2} = 4

-et behelyettesítve

(2')

-be, majd a

(3')

-be:

\begin{matrix} x = \frac{a^{2} - 5}{2 a} és y = \sqrt[]{4 - x^{2}} = \sqrt[]{4 - {(\frac{a^{2} - 5}{2 a})}^{2}} . \end{matrix}

x

és

y

most kapott kifejezéseit

(3')

-be helyettesítve az alábbi negyedfokú egyenletet kapjuk

a

-ra:

\begin{matrix} 4 a^{4} - 152 a^{2} + 1444 = 0, \end{matrix}

ahonnan a háromszög oldala

a = \sqrt[]{19} \approx 4,359

egység.

Bakonyi Zoltán (Bp., Veres Péter Gimn., IV. o.t.)

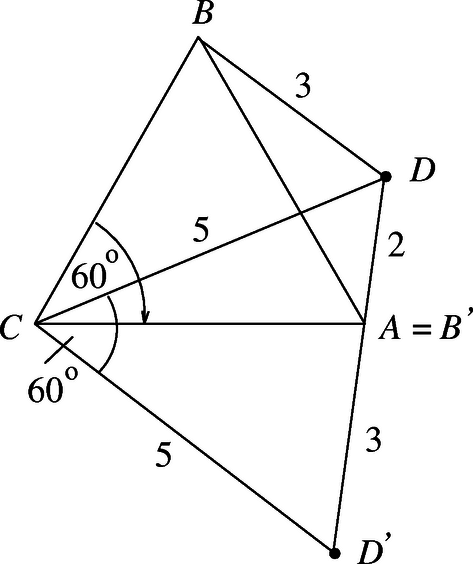
II. megoldás. Rajzoljuk meg az

A B C

háromszöget és a rajta kívül fekvő

D

pontot, amelyre

A D = 2

B D = 3

C D = 5

.
Forgassuk el a

C B D

háromszöget a

C

pont körül

60^{\circ}

-kal úgy, hogy

B

elforgatottja,

B'

A

pontba kerüljön,

D

képe

D'

. Így

C D = C D' = 5

, a

D C D'

háromszög egyenlő szárú, és mivel

D C D' ∢ = 60^{\circ}

, így

C D' D ∢ = D' D C ∢

60^{\circ}

-osak. Tehát a

D C D'

háromszög egyenlő oldalú,

D D' = 5

. De

D A + A D' = 2 + 3 = 5

, vagyis

D

A

D'

egy egyenesbe esik, és

A D' C ∢ = 60^{\circ}

. Az

A D' C

háromszög

A C = a

oldalára írjuk fel a koszinusztételt:

\begin{matrix} a^{2} = 3^{2} + 5^{2} - 2 \cdot 3 \cdot 5 \cdot cos 60^{\circ}, \end{matrix}

ahonnan

a = \sqrt[]{19}

, amint azt már az előbb is láttuk.

Fazekas Péter (Bp., Apáczai Cs. J. Gimn., III. o.t.)

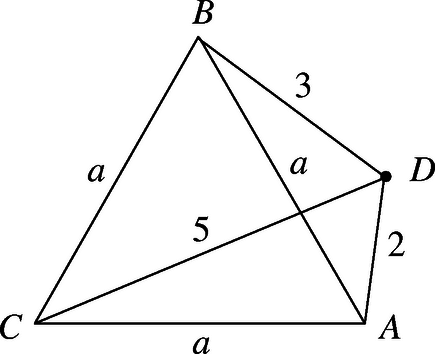
III. megoldás. A Ptolemaiosz-tétel azt mondja ki, hogy egy húrnégyszögben az átlók szorzata egyenlő a szemközti oldalpárok szorzatainak összegével. A tétel megfordítása is igaz, vagyis ha egy négyszög átlóinak szorzata egyenlő a szemközti oldalpárok szorzatainak összegével, akkor a négyszög húrnégyszög. (A tétel és bizonyítása megtalálható pl. H. S. M. Coxeter‐S. L. Greitzer: Az újra felfedezett matematika, 74. old., Gondolat Kiadó, Budapest, 1977.)
Esetünkben

5 a = 2 a + 3 a

, vagyis

A D B C

húrnégyszög, és mivel

A C B ∢ = 60^{\circ}

B D A ∢ = 120^{\circ}

. A

B D A

háromszögben írjuk fel a koszinusztételt:

\begin{matrix} a^{2} = 2^{2} + 3^{2} - 2 \cdot 2 \cdot 3 \cdot cos 120^{\circ} = 2^{2} + 3^{2} + 6 = 19, \end{matrix}

így

a = \sqrt[]{19}

Zaupper Bence (Győr, Krúdy Gy. Szki., III. o.t.)