Feladat: 1966. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1967/április, 148 - 149. oldal  PDF  |  MathML 
Témakör(ök): Húrnégyszögek, Középvonal, Magasságvonal, Arany Dániel
Hivatkozás(ok):Feladatok: 1967/április: 1966. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Messe a kérdéses merőleges a-t G-ben, b-t H-ban, ekkor elég belátnunk az FGH és FHG szögek egyenlőségét, hiszen így FGH egyenlő szárú háromszög, és FP magassága felezi a GH alapot. Válasszuk a betűzést úgy, hogy a és b közül a P-hez közelebbi legyen a.
Legyen először f az a és b közti négy szögtartomány közül annak a felezője, amelyikben P benne van, és messe az t-re merőleges PA egyenes b-t B-ben. P az AB szakaszon van, F ugyanebben a szögtartományban adódik, és G az FP egyenesnek azon a partján, amelyiken A van, B és H pedig a másik partján. FPAG és FPHB húrnégyszögek, mert az FG szakasz A-ból és P-ből, FH pedig P-ből és B-ből derékszögben látszik, hiszen B az A tükörképe f-re, és így FB merőleges b-re. Mivel még P a GH szakasz belső pontja, azért

FGH∢=FGP∢=FAP∢=FBP∢=FHP∢=FHG∢.

Ezt akartuk bizonyítani, ebből ‐ mint láttuk ‐ az állítás egyszerűen következik.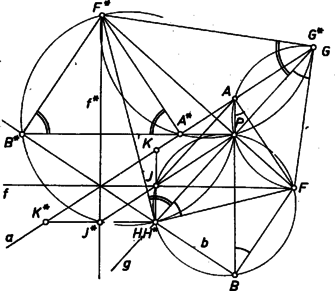
 
 

f-ként a P-t tartalmazó a, b szögtartománnyal szomszédos szögtartományok felezőjét véve ‐ legyen ez f*, és az így szerkesztett pontok A*, F*, G*, H* és B*, meggondolásunk csak abban változik, hogy F*P szétválasztja az A*, G* pontpárt és hogy A* van a PB* szakaszon. A megfelelő húrnégyszögekből ekkor is

F*G*H*∢=F*G*P∢=180∘-F*A*P∢=F*A*B*∢=F*B*A*=F*B*P∢=F*H*P∢=F*H*G*∢.



Ezzel a bizonyítást befejeztük.
 
II. megoldás. Az állítás fordítottját bizonyítjuk, megmutatjuk, hogy ha P felezi a g egyenesnek az a és b közé eső GH szakaszát, akkor FP merőleges g-re. Ebből az állítás akkor következik, ha azt is belátjuk, hogy P a rajta átmenő egyenesek közül csak egynek felezi az a és b közti szakaszát. Ez abból adódik, hogy pl. G-t b-nek P-re vett tükörképe metszi ki a-ból.
Messe a H-n átmenő, f-re merőleges egyenes f-et J-ben, a-t K-ban. H és K tükrös pár f-re, ezért J felezi HK-t, és mivel még HK∥AP, azért PAJ a KHG háromszög középháromszöge, PJ∥a és AJ∥g. Így F a PAJ háromszög magasságpontja, hiszen itt metszi egymást a J-ből és A-ból kiinduló magasságvonal. Ezért PF merőleges AJ-re és a vele párhuzamos g-re is, amint állítottuk.
Ezzel a bizonyítást befejeztük. Bizonyításunk mindkét szögfelezőre egyformán érvényes.