Feladat: 1966. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1967/január, 3 - 4. oldal  PDF  |  MathML 
Témakör(ök): Számjegyekkel kapcsolatos feladatok, Arany Dániel
Hivatkozás(ok):Feladatok: 1967/január: 1966. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a keresett kétjegyű számok egyike xy¯=10x+y. Ekkor a feladat feltétele szerint

10x+y=7⋅(x+y)+6,
és itt
6<x+y,(1)
továbbá x és y olyan egész számok, amelyekre
1≦x≦9,0≦y≦9.(2)

Az egyenlet átrendezése után
x=2y+2.(3)

Ezt a kifejezést (1)-be helyettesítve egyrészt
3y+2>6,azazy>43,
másrészt (2) és (3) alapján
2y+2≦9,azazy≦72.

Mivel y egész, ezért mind a két korlátnak csak a 2 és 3 érték tesz eleget, y=2-höz x=6, y=3-hoz x=8 tartozik, és így a keresett kétjegyű számok 62 és 83. Ezek ki is elégítik a feladat követelményeit.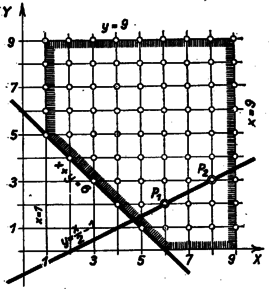
 
 
2. ábra
 

Megjegyzések. 1. Az x, y egész számokat egy P pont derékszögű koordinátáinak tekintve, értékeik grafikusan is meghatározhatók. A szóba jöhető P pontok helyét az (1) és (2) egyenlőtlenségek, továbbá az (1) egyenlet szabja meg. A (2) egyenlőtlenségek azt jelentik hogy a P pontok csak az x=1 egyenestől jobbra, az x=9 egyenestől balra (2. ábra), az y=0 egyenes fölött és az y=9 egyenes alatt, vagy a határoló egyeneseken lehetnek. (1) szerint pedig a P pontok az x+y=6 egyenestől a nagyobb ordináták irányába eshetnek. A P pontok lehetséges helyét vonalkázással jelöltük. Végül (3) azt jelenti, hogy a P pontok csak az
y=x2-1
egyenes egész koordinátájú pontjai lehetnek. Az ábrából leolvasható, hogy minden feltételnek eleget tevő pont csak kettő van, a P1(6,2) és P2(8,3), tehát a keresett számok 62 és 83.
 
2. Számos versenyző tévesen a 20 és 41 számokat is megoldásnak vette, mert 20=2⋅7+6 és 41=5⋅7+6, és nem gondolt arra, hogy az osztás maradéka nem lehet nagyobb az osztónál.