Kezdőlap


Feladat:	1965. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1966/március, 100 - 101. oldal		PDF \| MathML
Témakör(ök):	Egyenes, Háromszögek hasonlósága, Deltoidok, Thalesz-kör, Arany Dániel
Hivatkozás(ok):	Feladatok: 1966/március: 1965. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Csak a kör $O$ középpontjától különböző $P$ pontok esetével kell foglalkoznunk, mert ha $P$ egybeesik $O$ -val, akkor $Q$ semmilyen helyzetében nem jön létre az $M$ metszéspont. Nem jön létre az $M$ pont akkor sem, ha $P$ különbözik $O$ -tól, de $Q$ a körből $O P$ -vel kimetszett $U V$ átmérő bármelyik végpontjában van.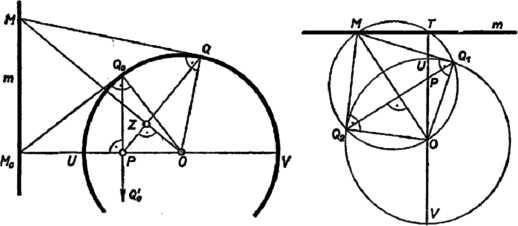
Megszerkesztve $M$ -et $Q$ néhány helyzetéhez, a kapott pontok egy egyenesbe esnek, amely merőleges $O P$ -re. Megmutatjuk, hogy a mértani hely valóban egyenes.

A mértani helynek van pontja az

O P

egyenesen. Akkor kapjuk ezt, amikor az

O

-n át

P Q

-ra állított merőleges maga

O P

, vagyis amikor

P Q

merőleges

O P

-re, más szóval

Q

a kör

P

-n átmenő,

O P

-re merőleges

Q_{0} Q'_{0}

húrjának valamelyik végpontjában van. Legyen a

Q_{0}

-hoz és

Q'_{0}

-höz tartozó pont

M_{0}

. Ekkor az

O Q_{0} M_{0}

és

O P Q_{0}

derékszögű háromszögek hasonlók, mert

O

-nál levő szögük közös, így

\begin{matrix} M_{0} O : Q_{0} O = Q_{0} O : P O, M_{0} O \cdot P O = Q_{0} O^{2} . \end{matrix}

(2)

M_{0}

O P

félegyenesen van.
Legyen a körnek egy az

U

V

Q_{0}

Q'_{0}

pontoktól különböző pontja

Q

, és messe

O M

P Q

egyenest

Z

-ben. Az

O Q M

és

O Z Q

háromszögekből az előbbiekhez hasonlóan, majd felhasználva (2)-t

\begin{matrix} M O \cdot Z O = Q O^{2} = Q_{0} O^{2} = M_{0} O \cdot P O, tehát \\ M O : M_{0} O = P O : Z O . \end{matrix}

A két egyenlő arány tagjai az

M M_{0} O

és

P Z O

háromszögek

O

-ból kiinduló oldalai. E háromszögek

O

-nál levő szöge közös, így hasonlók, ezért

M M_{0} O ∢ = P Z O ∢ = 90^{\circ}

. Ezzel beláttuk, hogy

M

valóban mindig az

M_{0}

-ban

O M_{0}

-ra, vagyis

O P

-re merőlegesen álló

m

egyenesen van.

m

minden pontja hozzátartozik a mértani helyhez. Láttuk ugyanis, hogy

M_{0}

a kört befutó pont

Q_{0}

és

Q'_{0}

helyzeteihez tartozik hozzá. Legyen

m

-nek egy az

M_{0}

-tól különböző pontja

M^{*}

, és az

M^{*}

-ból a körhöz húzott egyik érintő érintési pontja

Q^{*}

. Ez csak

M^{*}

-ot szolgáltathatja, mert

U

-tól és

V

-től különbözik,

m

-en levő pontot szolgáltat, de a

Q^{*}

-ban húzott érintő egyetlen közös pontja

m

-mel

M^{*}

, tehát

M^{*}

valóban hozzátartozik a mértani helyhez.
Mindezek szerint a keresett mértani hely az

O P

félegyenesre a (2)-nek eleget tevő

M_{0}

pontjában állított merőleges.

II. megoldás.

P

-n át tetszés szerinti, de

O

-n át nem menő egyenest húzva, ennek a körrel való

Q_{1}

Q_{2}

metszéspontjaihoz közös

M

pont tartozik. Ugyanis

M

-mel a

Q_{1}

-beli és

Q_{2}

-beli érintők metszéspontját jelölve az

M Q_{1} O Q_{2}

négyszög deltoid, mert

O

-ból kiinduló oldalai, valamint a végpontjaiknál levő szögek egyenlők, tehát

M O

átlója merőleges a

Q_{1} Q_{2}

átlóra. Ez pedig azonos a

P Q_{1}

P Q_{2}

egyenessel, tehát az előírás szerint

Q_{1}

-hez és

Q_{2}

-höz

M

tartozik hozzá.
A deltoid köré kör írható, mert a szemben fekvő

Q_{1}

Q_{2}

csúcsainál levő szögek összege két derékszöggel egyenlő, így

M O

e körben átmérő. Messe ez

a

kör az

O P

egyenest másodszor

T

-ben, így Thalész tétele szerint az

O T M

szög derékszög.
Könnyű belátni, hogy

T

helyzete független a

Q_{1} Q_{2}

egyenes megválasztásától. A deltoid köré írt körnek

T O

és

Q_{1} Q_{2}

P

-n átmenő húrjai, így

\begin{matrix} P T \cdot P O = P Q_{1} \cdot P Q_{2} . \end{matrix}

Hasonlóan az adott körből

\begin{matrix} P Q_{1} \cdot P Q_{2} = P U \cdot P V, \end{matrix}

ahol

U

V

ismét az adott körnek

P O

-n levő pontjai, így

\begin{matrix} P T \cdot P O = P U \cdot P V . \end{matrix}

Itt

P O

P U

és

P V

állandó, tehát

P T

is állandó, amint állítottuk.
Ezek szerint

M

mindig az

O P

egyenesre az állandó

T

pontban állított

m

merőlegesen van.
Eredményünk alapján

m

M

egyetlen helyzetéből megszerkeszthető. Ha pl. a

P

-n át választott egyenes merőleges

O P

-re, akkor

M

O P

-n, tehát éppen

T

-ben adódik.
Az I. megoldáshoz hasonlóan látható be, hogy

m

minden pontja a mozgó pont egy helyzetéhez tartozik,

m

a keresett mértani hely.