Feladat: 1965. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 2. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1966/március, 98 - 99. oldal  PDF  |  MathML 
Témakör(ök): Beírt kör, Egyenlő szárú háromszögek geometriája, Középponti és kerületi szögek, Arany Dániel
Hivatkozás(ok):Feladatok: 1966/március: 1965. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az adott egyenlő szárú trapéz ABCD, ahol a csúcsokat úgy betűztük, hogy AB‖CD és AB≥CD álljon. Jelöljük az ABC háromszögbe írt kör középpontját O-val, a BCD háromszögbe írtét Q-val, az előbbi kör érintési pontját AB-n S-sel, az utóbbiét CD-n Z-vel. A feladat állítása igazolást nyer azzal, ha megmutatjuk, hogy SZ merőleges a párhuzamos oldalakra, hiszen O az AB-re S-ben emelt merőlegesen van, Q pedig a CD-re Z-ben állított merőlegesen. D vetületét AB-n T-vel jelölve azt mutatjuk meg, hogy DTSZ téglalap. Ehhez elég megmutatni, hogy DZ=TS, hiszen ez a két oldal párhuzamos és merőleges 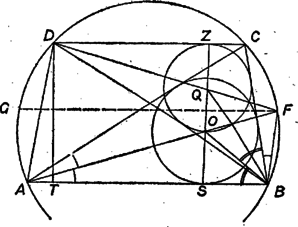DT-re.
A háromszög csúcsainak a beírt kör érintési pontjától való távolsága és az oldalak hossza közti ismert összefüggés szerint

AS=12(AB+AC-BC),DZ=12(DC+DB-BC).
A T pont az AB szakaszon van (esetleg egybeesik A-val), így a TS szakasz, figyelembe véve, hogy az átlók egyenlők,
 
 


TS=AS-AT==12(AB+DB-BC)-12(AB-CD)==12(DB+CD-BC)=DZ,


DTSZ tehát valóban téglalap. (Nem lehet, hogy O és Q egybeessék, s így a rajtuk átmenő egyenes iránya határozatlan, mert akkor a körök is egybeesnének, hiszen mindkettő érinti BC-t; de pl. az ABC háromszögbe írt kör nem érintheti CD-t, mert CD-nek C az egyetlen közös pontja a háromszöggel, az pedig a körön kívül van.
 
Megjegyzés. Hasonlóan lehet belátni, hogy a BCA és BOD háromszög külső érintő köreinek középpontjai ‐ alkalmas páronként összekötve ‐ ugyancsak az AB-re merőleges egyeneseket adnak.
 
II. megoldás. Az előző megoldás jelöléseit használjuk. A trapéz köré kör írható. Legyen a kör A-t (és D-t) nem tartalmazó BC ívének felezőpontja F. Megmutatjuk, hogy az OFQ háromszög egyenlő szárú és OQ-ra merőleges szimmetriatengelye párhuzamos a trapéz párhuzamos oldalaival. Ezzel a feladat állítása bizonyítást nyer.
Az állítás első része abból következik, hogy OFB és QFB egyenlő szárú háromszögek. AO és BO szögfelezők, és előbbi átmegy F-en. Így, felhasználva a külső szög és a kerületi szög tételét:
FOB∢=FAB∢+OBA∢=FAC∢+OBC∢==FBC∢+CBO∢=FBO∢.


Hasonlóan látható a QFB háromszög egyenlő szárú volta is. A kettőből OF=BF=QF, tehát OFQ is egyenlő szárú háromszög. Szimmetriatengelye az OFQ∢=AFD∢ felezője, átmegy a B-t nem tartalmazó AD ív G felezőpontján. Ez az F pont tükörképe a trapéz szimmetriatengelyére, így FG valóban párhuzamos a párhuzamos oldalakkal, OQ tehát merőleges rájuk.