Kezdőlap


Feladat:	1965. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1966/május, 198 - 199. oldal		PDF \| MathML
Témakör(ök):	Thalesz-kör, Középponti és kerületi szögek, Arany Dániel
Hivatkozás(ok):	Feladatok: 1966/május: 1965. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C D$ konvex négyszög $A$ , $B$ és $C$ csúcsánál levő szöge tompaszög. Írjunk kört az $A$ , $B$ , $C$ csúcsok köré, ennek $B$ -vel átellenes pontja legyen $B'$ . Ez a $B A D$ szögtartománynak is, a $B C D$ szögtartománynak is a belsejében van, ugyanis Thalész tétele szerint $B A B' ∢ = B C B' ∢ = 90^{\circ}$ , az $A B'$ és $C B'$ félegyenes ís a megfelelő szögtartomány belsejében halad. Ebből következik, hogy a $B B' D$ konvex szög a $B A D ∢$ , $B O D ∢$ egyikénél nagyobb, tehát tompaszög. Igy a $B B' D$ háromszög legnagyobb oldala nagyobb $B B'$ -nél, ez pedig, mint körátmérő, nem kisebb a kör $A C$ húrján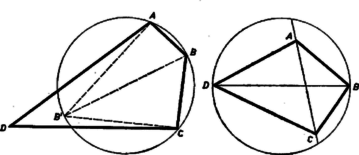ál.

II. megoldás. Az előző megoldás jelöléseit és feltételeit használjuk. Rajzoljunk kört a

B D

átló mint átmérő fölé. Azok a pontok, amelyekből

B D

tompaszögben látszik, a kör belsejében vannak, így

A

és

C

is.

A C

tehát a kör belsejében levő szakasz, s így kisebb, mint a kör átmérője,

B D

Megjegyzés. Csak azt használtuk fel mind a két megoldásban, hogy

A

-nál és

C

-nél tompaszög van. Ebből a négyszög konvex volta is következik. Így azt bizonyítottuk be, hogy ha egy négyszög két szemben fekvő szöge tompaszög, akkor az ezek csúcsát összekötő átló rövidebb a másik átlónál.