Kezdőlap


Feladat:	1965. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1966/február, 49 - 52. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Transzformációk szorzata, Arany Dániel
Hivatkozás(ok):	Feladatok: 1966/február: 1965. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vázlatot készítve azt találjuk, hogy a kérdéses metszéspont a körön van. Könnyebb lesz ezt a többet mondó állítást bebizonyítani.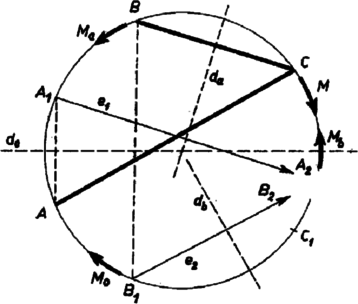

1. ábra

Mivel átmérőre tükröztünk,

A_{1}

B_{1}

és

C_{1}

is a körön van. Azt fogjuk megmutatni, hogy az

A_{1}

-en át

B C

-vel és a

B_{1}

-en át

A C

-vel párhuzamosan húzott

e_{1}

, illetőleg

e_{2}

egyenes a körön metszi egymást. A harmadik egyenesre már könnyen átvihető lesz eredményünk.
Messe az

e_{1}

egyenes a kört másodszor

A_{2}

-ben, az

e_{2}

egyenes

B_{2}

-ben, így azt akarjuk belátni, hogy

A_{2}

azonos

B_{2}

-vel. Egyelőre feltesszük, hogy

A_{1}

és

A_{2}

különböző pontok, úgyszintén

B_{1}

és

B_{2}

is (1. ábra).
A

B C

és

A_{1} A_{2}

szakaszok a kör párhuzamos húrjai, ezért végpontjaik egy szimmetrikus trapéz (húrtrapéz) csúcsai, páronként egymás tükörképei a mindkét húrra merőlegesen álló

d_{a}

átmérőre mint tengelyre nézve. Így a

C A_{2}

és

B A_{1}

húrok egyenlők, mert egymás

d_{a}

-ra vonatkozó tükörképei. Hasonlóan egy húrtrapéz csúcsai az

A

A_{l}

B

és

B_{1}

pontok ‐ az először végzett tükrözések miatt, mert

A A_{1}

és

B B_{1}

merőlegesek a felhasznált

d_{0}

átmérőre ‐, valamint

A

C

B_{1}

és

B_{2}

is, a másodszorra szerkesztett párhuzamos miatt, itt a szimmetriatengely az

A C

-re merőleges

d_{b}

átmérő. Ezért

\begin{matrix} B A_{1} = B_{1} A = B_{2} C és így C A_{2} = B_{2} C \end{matrix}

(1)

Eszerint

A_{2}

és

B_{2}

a körnek

C

-től egyenlő távolságra levő pontjai, tehát vagy egymás tükörképei a

C

-ből kiinduló átmérőre nézve, vagy egybeesnek. Csak azt kell már belátnunk, hogy az utóbbi eset áll fenn.
Mozgassunk egy

M

pontot a körön

C

-ből

A_{2}

-be a köztük levő két körív valamelyikén, és tekintsük azt a mozgást, amit

M

-nek

d_{a}

-ra való

M_{a}

tükörképe végez, továbbá

M_{a}

-nak

d_{0}

-ra való

M_{0}

tükörképe, végül amit

M_{0}

-nak

d_{b}

-re való

M_{b}

tükörképe végez. Az (1) alatti egyenlő húrok mindegyikének végpontjai a kört úgy osztják két-két ívre, hogy a részívek páronként egyenlők, és az

M

M_{a}

M_{0}

M_{b}

pontok az egyenlő hosszú íveket írják le. A pontok mozgása mindig a kör középpontja körüli forgás, amelynek iránya az egymás utáni párokban a tükrözés miatt ellentétes. Igy

M

és

M_{0}

forgási iránya megegyező, mert mindegyik ellentétes irányú

M_{a}

forgásával, és hasonlóan

M_{b}

iránya is ellentétes

M

-ével. Ezért az

M

és

M_{b}

által befutott

C A_{2}

és

B_{2} C

ívek ellentétes irányúak, az utóbbinak a végpontja viszont azonos az előbbinek a kezdőpontjával, ezért a

B_{2}

kezdőpont is azonos az

A_{2}

végponttal. Ezt akartuk belátni.
Akkor is érvényes (1), valamint meggondolásunk záró része is, ha

e_{1}

érinti a kört. Ekkor ugyanis

A_{2}

helyén csak maga

A_{1}

vehető, másrészt az

A_{1}

-ből kiinduló átmérő merőleges

B C

-re, az

A_{1} B C

háromszög egyenlő szárú, és így

C A_{2} = C A_{1} = B A_{1}

. Hasonlóan okoskodunk, ha

e_{2}

érinti a kört. Ezzel az első két párhuzamosra vonatkozó állításunkat bebizonyítottuk.
Meggondolásunkban az

A

B

C

;

A_{1}

B_{1}

;

A_{2}

B_{2}

pontok szerepét rendre a

B

C

A

B_{1}

C_{1}

B_{2}

C_{2}

pontoknak adva át, úgyszintén

e_{1}

e_{2}

d_{a}

d_{b}

M_{a}

M_{b}

szerepét rendre

e_{2}

e_{3}

d_{b}

d_{c}

M_{b}

M_{c}

-nek ‐ ahol

C_{2}

-t,

e_{3}

-at,

d_{c}

-t és

M_{c}

-t a fentiekhez hasonlóan értelmezzük ‐, azt kapjuk, hogy

e_{2}

és

e_{3}

a körön metszik egymást,

C_{2}

egybeesik

B_{2}

-vel, tehát az eredeti meggondolás szerint

A_{2}

-vel is. Ezzel állításunkat bebizonyítottuk.

Megjegyzés.

M

és tükörképei mozgásának elképzelése tulajdonképpen mellőzhetővé tette az (1)-re vezető meggondolást, hiszen megismételte azt, de többet mondott nála. Az ábra azonban csak nyugalmi helyzetet mutat, szemlélete előkészítette a később mondottakat.

II. megoldás. Ismét azt bizonyítjuk, hogy a feladatban szereplő egyenesek a körön metszik egymást. Elég megmutatni, hogy az

A_{1}

-en át

B C

-vel és

B_{1}

-en át

A C

-vel húzott párhuzamosok a körön metszik egymást. A feltételeket leírhatjuk csupán a kör

O

középpontján átmenő tengelyekre való tükrözésekkel.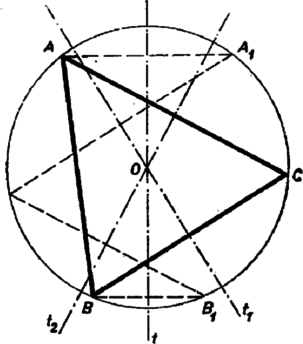

2. ábra

Jelöljük a körnek a feladat szövegében említett átmérőjét

t

-vel, a

B C

-re és a

C A

-ra merőleges átmérőt

t_{1}

-gyel, ill.

t_{2}

-vel (2. ábra). Ekkor

A

-ból a kérdéses körpontba úgy juthatunk, hogy

A

-t tükrözzük

t

-re, majd a tükörkép-pontot (

A_{1}

-et)

t_{1}

-re; hasonlóan

B

-ből a megfelelő metszéspontba a

t

-re, majd

t_{2}

-re való tükrözéssel juthatunk. Megfordítva, a kétszeri tükrözéssel kapott pontból

B

-be a

t_{2}

-re, majd

t

-re való tükrözéssel jutunk ‐ és csak ebből a pontból, hiszen

B_{1}

az egyetlen pont, amelyet

t

-re tükrözve

B

-t kapjuk, és olyan pont is egyetlenegy van, amelynek

t_{2}

-re vonatkozó tükörképe

B_{1}

, ugyanis

B_{1}

-nek a

t_{2}

-re vonatkozó tükörképe. Így, ha állításunk igaz, akkor

A

-t sorra tükrözve

t

-re,

t_{1}

-re,

t_{2}

-re, majd újra

t

-re,

B

-be jutunk, de fordítva is, ha utolsó állításunk igaz, akkor

A

-t

t

-re, majd

t_{1}

-re tükrözve ugyanazt a pontot kapjuk, mint ha

B

-t tükrözzük

t

-re, majd

t_{2}

-re.
Elég tehát azt megmutatni, hogy

A

a fent említett négy tükrözéssel

B

-be megy át.
Ehhez megmutatjuk, hogy két egymást metsző tengelyre történő, egymás utáni tükrözés eredménye ugyanaz, mint ha metszéspontjuk körül egy kétszer akkora forgatást végzünk, mint ami az első tükrözés tengelyét a másodikéba viszi át.
Ebből átfogalmazott állításunk helyessége következik, hiszen

A

-t a t, majd. a

t_{1}

tengelyre tükrözve az eredmény a kör

O

középpontja körül a

t

-t

t_{1}

-be vivő forgás kétszeresével való elforgatással helyettesíthető. Az ez utáni tükrözés

t_{2}

-re, majd

t

-re annak a forgatásnak a kétszeresével helyettesíthető, amely

t_{2}

-t

t

-be viszi át. A két forgatást egymás után elvégezve a forgatások szögei összeadódnak, és ez a forgásszög-összeg független a forgatások sorrendjétől. Így a négy tükrözés együtt annak a forgatásnak a kétszeresét adja, amellyel

t_{2}

, a

t

-be, majd innen

t_{1}

-be forgatható. Az utoljára említett forgatás a

t_{2}

-t

t_{1}

-be vivő forgatás, vagy ennél

180^{\circ}

egy többszörösével nagyobb. Így kétszerese a

t_{2}

-t

t_{1}

-be vivő forgatás kétszeresétől csak

360^{\circ}

egy többszörösével különbözhet, azonban

360^{\circ}

egy többszörösével való forgatás minden pontot önmagába visz át.
A négy egymás utáni tükrözés eredménye tehát az

O

körül a

t_{2}

-t

t_{1}

-be vivő forgatás kétszerese, ez pedig

A

-t éppen

B

-be viszi át; ezt akartuk bizonyítani.
A két tükrözés összetételére vonatkozó állítást kell tehát még belátnunk. Legyen a két egymást metsző tükörtengely

a

és

b

, metszéspontjuk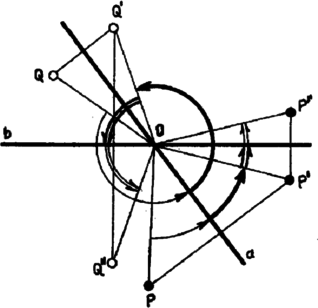

O

3. ábra

Egy

P

pont

a

-ra vonatkozó tükörképét megkaphatjuk úgy is, hogy az

O P

szakaszt

O

körül pl. az óramutató járásával ellentétes irányban ‐ ezt szokás pozitív forgásiránynak tekinteni ‐

a

-ig forgatjuk, majd innen ugyanekkora szöggel tovább. az

O P'

helyzetbe. Ekkor

P'

P

tükörképe

a

-ra (3. ábra). A

P

-t

P'

-be vivő forgás szöge függ

P

helyzetétől.

P'

-t a

b

-re vonatkozó

P "

tükörképébe ismét átvihetjük úgy, hogy

O P'

-t pozitív irányban

b

-ig forgatjuk, majd innen még ugyanekkora szöggel továbbforgatva jutunk az

O P "

szakaszhoz. Így végül

O P

-t annak a forgásnak a kétszeresével forgattuk el (a 3. ábra vastagabban jelölt ívei), amely

a

-t

P'

-n áthaladva

b

-be viszi át. Ez vagy az

a

-t pozitív irányban

b

-be vivő legkisebb forgás, vagy az annál

180^{\circ}

-kal nagyobb forgás kétszerese; eredménye tehát minden esetben ugyanaz, mint az

a

-t

b

-be vivő forgatás kétszereséé, mért a

360^{\circ}

-kal való továbbforgatás nem okoz változást. Ezzel segédtételünket, s így a feladat állítását is bebizonyítottuk.

Megjegyzések. 1. Itt nem kellett különválasztanunk azt az esetet, ha pl. az

A_{1}

-en át

B C

-vel párhuzamosan húzott egyenes érinti a kört. Ekkor

t_{1}

átmegy

A_{1}

-en, s így a rá való tükrözés

A_{1}

-et helyben hagyja.
2. Meggondolásunkban felhasználtuk, hogy egy középpont körüli egymás utáni forgatások felcserélhetők, így segédtételünk értelmében egy ponton átmenő tengelyekre vonatkozó tükrözéspárok is felcserélhetők. (Tükrözések nem cserélhetők fel, hiszen a

b

-re, majd

a

-ra való tükrözés azt a forgást adja, ami az

a

-ra, majd

b

-re való tükrözéssel egyenértékű forgatást teljes körülforgássá egészíti ki.) Így a

t

-re,

t_{1}

-re,

t_{2}

-re, majd

t

-re vonatkozó tükrözés ugyanazt eredményezi, mint ha

t_{2}

-re,

t

-re, újra

t

-re, majd

t_{1}

-re tükrözünk. Azonban a

t

-re való kétszeri tükrözés minden pontot helyben hagy, tehát az eredmény ugyanaz, mint ha

t_{2}

-re, majd

t_{1}

-re tükrözünk. Lényegében ezt láttuk be a megoldás során geometriailag.
3. A bizonyítandó állítást tovább alakíthatjuk, megfigyelve, hogy

B

-t ismét

t_{1}

-re, majd

t_{2}

-re tükrözve

C

-be, majd

A

-ba jut, és

B

az egyetlen pont, aminek megvan ez a tulajdonsága. Elég tehát azt megmutatni, hogy

A

-t sorra a

t

t_{1}

t_{2}

t

t_{1}

t_{2}

tengelyekre tükrözve eredeti helyzetébe jut vissza. Ez azonnal látható, ha ‐ előző megjegyzésünk értelmében ‐ az első és második tükrözéspárt megcseréljük. Eszerint a hat tükrözés eredménye ugyanaz, mintha,

A

-t sorra a

t_{2}

t

t

t_{1}

t_{1}

t_{2}

tengelyekre tükrözzük. De a

t

-re és újra

t

-re való tükrözés helyben hagyást eredményez, úgyszintén a

t_{1}

-re és ismét

t_{1}

-re való tükrözés, tehát a hat tükrözés egymásutánja ugyanazt eredményezi, mint a

t_{2}

-re, majd

t_{2}

-re való tükrözés, vagyis a helyben hagyást.
4. Az előző átfogalmazás azt jelenti, hogy a

t

t_{1}

t_{2}

tengelyekre való tükrözések egymásutánja olyan transzformációt eredményez, amelyet kétszer egymásután alkalmazva minden pont eredeti helyzetébe kerül vissza. Valóban, a három tükrözés eredménye egyetlen tükrözéssel helyettesíthető. A

t

-re és

t_{1}

-re való tükrözés ugyanis annak a forgatásnak a kétszeresével helyettesíthető, amelyik

t

-t pozitív irányban

t_{1}

-be viszi át. Ugyanerre a forgatásra vezet azonban minden olyan

O

-n átmenő tengelypárra vonatkozó tükrözés is, amelyek elsőjét a másodikba ugyanakkora forgás viszi át, mint

t

-t

t_{1}

-be. Legyen

t *

az a tengely, amelyet

t_{2}

-be ugyanaz a forgatás viszi át, mint

t

-t

t_{1}

-be. Ekkor a

t

-re,

t_{1}

-re, majd

t_{2}

-re való tükrözés eredménye ugyanaz, mint a

t *

-ra,

t_{2}

-re, majd

t_{2}

-re való tükrözésé, ezé pedig ugyanaz, mint a

t *

-ra való tükrözésé. Ezzel állításunkat igazoltuk.