Kezdőlap


Feladat:	1964. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1965/február, 55 - 56. oldal		PDF \| MathML
Témakör(ök):	Téglalapok, Thalesz-kör, Szögfüggvények, síkgeometriai számítások, Arany Dániel
Hivatkozás(ok):	Feladatok: 1964/szeptember: 1964. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen egy az $A B C$ háromszög köré írható, $A$ csúcsú téglalapok közül $A D E F$ úgy, hogy a $D E$ oldal $B$ -n, $E F$ pedig $C$ -n halad át (5. ábra). Így $B E C$ derékszög, ezért $E$ a $B C$ átmérő fölötti Thalész körön van, éspedig ennek azon a félkörén, amelyet a $B C$ egyenes elválaszt $A$ -tól. Jelöljük a kör középpontját ( $B C$ felezőpontját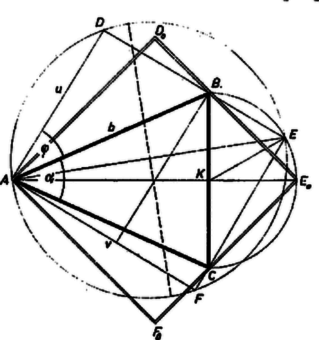) $K$ -val.

5. ábra

a) Megmutatjuk, hogy a keresett legnagyobb területű körülírt téglalapot akkor kapjuk, ha

E

a mondott félkörív

E_{0}

felezőpontjában adódik. Ekkor a körülírt

A D_{0} E_{0} F_{0} = N_{0}

téglalap négyzet, mert az

A E_{0}

egyenes merőleges

B C

-re, így felezi a

B E_{0} C ∢ = D_{0} E_{0} F_{0}

szöget.
Ha

A D E F = T

egy

N_{0}

-tól különböző, az

A B C

háromszög köré írt téglalap, akkor átlója rövidebb, mint

A E_{0}

, mert

\begin{matrix} A E < A K + K E = A K + \\ + K E_{0} = A E_{0} \end{matrix}

Így minden

A E

átlójú téglalap területe is kisebb, mint

N_{0}

-é, ugyanis e téglalapok másik két csúcsa az

A E

átmérőjű körön van, ennek pedig

A E

-től legtávolabbi pontjai az

A E

-re merőleges átmérő végpontjai, vagyis az egyenlő átlójú téglalapok közül a négyzet területe a legnagyobb; de még az

A E

átlójú négyzet területe is kisebb, mint

N_{0}

-é.

b) Az

A B C

háromszög keresett legkisebb területű körülírt téglalapját akkor kapjuk, ha a téglalap egyik oldala

A B

vagy

A C

(e két téglalap szimmetrikus az

A B C

háromszög tengelyére, így területeik egyenlők). Ekkor ugyanis a téglalap területe 2-szer akkora, mint az

A B C

háromszögé, és könnyű belátni, hogy körülírt téglalap területe ennél nem lehet kisebb. Ugyanis a

B

-n át

E F

-fel párhuzamosan húzott egyenes a körülírt téglalapot és az

A B C

háromszöget két részre vágja. Mindegyik rész‐téglalapba be van írva egy rész‐háromszög, amelyiknek egyik oldala a téglalap egy oldalán fekszik, és nem nagyobb ennél a téglalapoldalnál, az ehhez tartozó magasság a téglalap szomszédos oldala. Így a két rész‐téglalap területe nem kisebb a rész‐háromszögek területe 2-szeresénél, ugyanez áll tehát az

A B C

háromszögre és a köré írt téglalapra is. Épp kétszer akkora is csak akkor lehet a körülírt téglalap területe, mint a háromszögé, ha a téglalap egyik oldala egybeesik a háromszög egyik szárával.

II. megoldás. Használjuk ismét az I. megoldás jelöléseit, legyen továbbá

A C = A B = b

B A C ∢ = α

A D = u, A F = v

, és

B A D ∢ = φ

. Az utóbbi szög legkisebb értéke 0, ha ti.

T

egyik oldala

A B

; legnagyobb értéke

90^{\circ} - α

, ha ti.

T

egyik oldala

A C

\begin{matrix} 0^{\circ} ≦ = φ ≦ 90^{\circ} - α . \end{matrix}

(12)

T

területe, az

A B D

és

A C F

derékszögű háromszögek felhasználásával

\begin{matrix} t = u v = b cos φ \cdot b sin (α + φ), \end{matrix}

ugyanis

A C F ∢ = C A D ∢ = α + φ

.
A két szögfüggvény szorzatát a

sin z cos w = [sin (z + w) + sin (z - w)] / 2

azonosság alkalmazásával összeggé alakítjuk:

\begin{matrix} t = \frac{b^{2}}{2} [sin (α + 2 φ) + sin α] . \end{matrix}

(13)

A zárójelben csak az első tag változik, és (12)-t 2-vel szorozva, valamint mindenütt

α

-t hozzáadva a változó szögre

\begin{matrix} α ≦ + 2 φ = 180^{\circ} - α . \end{matrix}

(14)

A talált intervallum bal végpontja a feltevés szerint hegyesszög, jobb végpontja tompaszög, közrezárják

90^{\circ}

-ot. Itt veszi fel (13) első tagja a legnagyobb értékét, 1-et, tehát

φ

-nek a maximális

t

-t adó értékére

\begin{matrix} α + 2 φ = 90^{\circ} -ból \frac{α}{2} + φ = 45^{\circ}, \end{matrix}

vagyis

t_{m} a x

akkor adódik, ha

A D

A B C

háromszög

A E_{0}

tengelyével

45^{\circ}

-os szöget zár be. Ekkor a rá merőleges

A F

oldalegyenes is

45^{\circ}

-ot zár be

A E_{0}

-lal, a körülírt téglalap tükrös

A E_{0}

-ra, tehát négyzet.
Az

y = sin x

függvény a (14) intervallum (

α

90^{\circ}

) részintervallumában nő, (

90^{\circ}

180^{\circ} - a

) részintervallumában fogy, így (13) legkisebb értéke az

a

és

180^{\circ} - α

végpontokban felvett értékek kisebbike. A két végpontban

y = sin x

értéke egyenlő, tehát

t

-nek az

\begin{matrix} α + 2 φ = α, azaz φ = 0^{\circ} és az \\ α + 2 φ = 180^{\circ} - α, azaz φ = 90^{\circ} - α \end{matrix}

értékek esetén egyaránt minimuma van. Az első esetben

A D

azonos

A B

-vel (és

D

azonos

B

-vel), a másodikban

A F

azonos

A C

-vel (és

F

azonos

C

-vel).
Ezzel a legnagyobb és legkisebb területű körülírt téglalapok meghatározását befejeztük.