Feladat: 1964. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1965/február, 50 - 52. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Háromszögek hasonlósága, Középponti és kerületi szögek, Arany Dániel
Hivatkozás(ok):Feladatok: 1964/szeptember: 1964. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen F tükörképe AG felező merőlegesére F', az AG és F'H egyenesek metszéspontja M.
I. Vizsgáljuk először azt az esetet, amikor F, G, H sorra az A-ból B, C, D felé induló félegyenesen van. Ekkor az AC egyenes elválasztja a B és D pontokat és velük együtt az F és H pontokat is. Így az AC egyenes A és G pontjaival kettévágott körnek különböző ívein van F és H, F' pedig ugyanazon az íven van, mint F, mert FF'∥AG. Ebből következik, hogy M az AG húr belső pontja.
Legyen F tükörképe AG felező merőlegesére F', az AG és F'H egyenesek metszéspontja M.
I. Vizsgáljuk először azt az esetet, amikor F, G, H sorra az A-ból B, C, D felé induló félegyenesen van. Ekkor az AC egyenes elválasztja a B és D pontokat és velük együtt az F és H pontokat is. Így az AC egyenes A és G pontjaival kettévágott körnek különböző ívein van F és H, F' pedig ugyanazon az íven van, mint F, mert FF'∥AG. Ebből következik, hogy M az AG húr belső pontja.

 
 
1. ábra
 

Megmutatjuk, hogy az
AHM,ACD,F'GMésCAB(6)
háromszögek hasonlók, megfelelő szögeik egyenlők. Ebből már könnyen fog következni (6). A háromszögek megfelelő szögeire egyrészt
ACB∢̲=CAD∢̲=HAM∢̲=HAG∢=HF'G∢=MF'G∢̲;
az utolsó előtti és az azt megelőző szög azonos íven nyugvó kerületi szögek. Másrészt
AHM∢̲=AHF'∢=AGF'∢=MGF'∢̲=FAG∢=CAB∢̲==ACD∢̲.


A második és harmadik szög azonos íven nyugvó kerületi szögek, a negyedik és ötödik pedig egymás tükörképe.
A (6) alatti első és második háromszög hasonlóságából, illetőleg a harmadik és negyedik hasonlóságából a következő arányok egyenlősége olvasható le:
AHAM=ACAD,GF'GM=ACAB.
Innen, figyelembe véve, hogy GF' és AF egymás tükörképei, tehát egyenlők, kapjuk, hogy
AD⋅AH=AC⋅AM,AB⋅AF=AC⋅GM,
és a kettőt összeadva, mivel AM+MG=AG, adódik az (5) egyenlőség.
 

II. Megmutatjuk, hogy az (5) egyenlőség a kör minden helyzeténél érvényes marad, ha az A-tól B-vel, C-vel, ill. D-vel ellentétes irányban levő pontok távolságát negatívnak tekintjük. Ennek belátására forgassuk a kört az A pont körül pl. az óramutató járásával ellentétes irányban. A fenti bizonyítás nem alkalmazható már, ha a kör az AB oldalt érintő helyzetbe kerül (2. ábra). Ekkor AF=0, másrészt az ACD és AHG háromszögek hasonlók, mert egy szögük közös és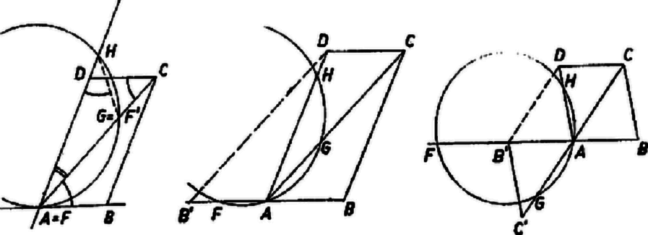
ACD∢=CAB∢=GAB∢=GHA∢.
Az utolsó egyenlőségben azonos íven nyugvó kerületi szögek szerepelnek. Így
ACAD=AHAG,AC⋅AG=AD⋅AH=AB⋅AF+AD⋅AH.

 
 
2.,  3.   és   4. ábra
 

Ha a kör továbbfordul, F az AB oldal A-n túli meghosszabbítására kerül (G és H még az AC és AD félegyeneseken lesz, 3. ábra). Jelöljük B-nek A-ra vonatkozó tükörképét B'-vel, ekkor az ACDB paralelogrammára érvényes az I. alatti bizonyítás és azt adja, hogy
AC⋅AG+AB'⋅AF=AD⋅AH,
azaz
AC⋅AG=AB⋅(-AF)+AD⋅AH.
Így ha magán az AF jelölésen a szakasz negatív előjellel vett hosszát értjük ebben az esetben, akkor az eredeti összefüggés változatlanul helyes marad.
Ha a kör továbbfordulásával G is az AC átló A-n túli meghosszabbítására kerül, akkor vegyük a B és C pontok A-ra vonatkozó B és C tükörképét. Az ADB'C' paralelogrammára ismét alkalmazható az I. rész bizonyítása, s így (4. ábra)
AC'⋅AG+AD⋅AH=AB'⋅AF.
azaz
AB⋅(-AF)+AD⋅AH=AC⋅(-AG).
Ez azonban ismét azt jelenti, hogy a II. elején mondott előjelmegállapodással (5) érvényben marad.
Ha a kör az AD-t A-ban érintő helyzeten is túlfordul, akkor korábban már tekintetbe vett körhelyzetek A-ra vonatkozó tükörképeit kapjuk. Egy ilyen tükrözés előjelmegállapodásunk szerint AF, AG és AH előjelének egyidejű megváltozását, és így (5) minden tagjának ellenkező előjelűre változását okozza, az egyenlőség helyességét tehát nem változtatja meg. Ezzel a II. alatti állítást is igazoltuk.
 

Megjegyzések. 1. Könnyen látható (1. ábra), hogy ABC▵∼FGH▵. A megfelelő szakaszok arányát h-val jelölve AB=h⋅GH, AC=h⋅FH, BC=AD=h⋅FG. Ezeket (5)-be beírva és h-val egyszerűsítve az AFGH húrnégyszögre a következő összefüggést kapjuk:
AF⋅GH+FG⋅HA=AG⋅FH,
vagyis húrnégyszögben a szemközti oldalpárok szorzatainak az összege az átlók szorzatával egyenlő. Ez az összefüggés PTOLEMAIOS tétele néven ismeretes. A fenti hasonlóság felhasználásával természetesen ebből a feladat állítása is könnyen következik. Ha viszont az I. alatti bizonyításban az ACD és CAB háromszög helyébe egyaránt az FHG háromszöget tesszük, akkor közvetlen bizonyítást kapunk PTOLEMAIOS tételére.
 

2. A versenyen a bíráló bizottság megelégedett az I. eset tárgyalásával.
Megmutatjuk, hogy az
AHM,ACD,F'GMésCAB(6)
háromszögek hasonlók, megfelelő szögeik egyenlők. Ebből már könnyen fog következni (6). A háromszögek megfelelő szögeire egyrészt
ACB∢̲=CAD∢̲=HAM∢̲=HAG∢=HF'G∢=MF'G∢̲;
az utolsó előtti és az azt megelőző szög azonos íven nyugvó kerületi szögek. Másrészt
AHM∢̲=AHF'∢=AGF'∢=MGF'∢̲=FAG∢=CAB∢̲==ACD∢̲.


A második és harmadik szög azonos íven nyugvó kerületi szögek, a negyedik és ötödik pedig egymás tükörképe.
A (6) alatti első és második háromszög hasonlóságából, illetőleg a harmadik és negyedik hasonlóságából a következő arányok egyenlősége olvasható le:
AHAM=ACAD,GF'GM=ACAB.
Innen, figyelembe véve, hogy GF' és AF egymás tükörképei, tehát egyenlők, kapjuk, hogy
AD⋅AH=AC⋅AM,AB⋅AF=AC⋅GM,
és a kettőt összeadva, mivel AM+MG=AG, adódik a (5) egyenlőség.
 

II. Megmutatjuk, hogy a (5) egyenlőség a kör minden helyzeténél érvényes marad, ha az A-tól B-vel, C-vel, ill. D-vel ellentétes irányban levő pontok távolságát negatívnak tekintjük. Ennek belátására forgassuk a kört az A pont körül pl. az óramutató járásával ellentétes irányban. A fenti bizonyítás nem alkalmazható már, ha a kör az AB oldalt érintő helyzetbe kerül (2. ábra). Ekkor AF=0, másrészt az ACD és AHG háromszögek hasonlók, mert egy szögük közös és
ACD∢=CAB∢=GAB∢=GHA∢.
Az utolsó egyenlőségben azonos íven nyugvó kerületi szögek szerepelnek. Így
ACAD=AHAG,AC⋅AG=AD⋅AH=AB⋅AF+AD⋅AH.

Ha a kör továbbfordul, F az AB oldal A-n túli meghosszabbítására kerül (G és H még az AC és AD félegyeneseken lesz, 3. ábra). Jelöljük B-nek A-ra vonatkozó tükörképét B'-vel, ekkor az ACDB paralelogrammára érvényes az I. alatti bizonyítás és azt adja, hogy
AC⋅AG+AB'⋅AF=AD⋅AH,
azaz
AC⋅AG=AB⋅(-AF)+AD⋅AH.
Így ha magán az AF jelölésen a szakasz negatív előjellel vett hosszát értjük ebben az esetben, akkor az eredeti összefüggés változatlanul helyes marad.
Ha a kör továbbfordulásával G is az AC átló A-n túli meghosszabbítására kerül, akkor vegyük a B és C pontok A-ra vonatkozó B és C tükörképét. Az ADB'C' paralelogrammára ismét alkalmazható az I. rész bizonyítása, s így (4. ábra)
AC'⋅AG+AD⋅AH=AB'⋅AF.
azaz
AB⋅(-AF)+AD⋅AH=AC⋅(-AG).
Ez azonban ismét azt jelenti, hogy a II. elején mondott előjelmegállapodással (5) érvényben marad.
Ha a kör az AD-t A-ban érintő helyzeten is túlfordul, akkor korábban már tekintetbe vett körhelyzetek A-ra vonatkozó tükörképeit kapjuk. Egy ilyen tükrözés előjelmegállapodásunk szerint AF, AG és AH előjelének egyidejű megváltozását, és így (5) minden tagjának ellenkező előjelűre változását okozza, az egyenlőség helyességét tehát nem változtatja meg. Ezzel a II. alatti állítást is igazoltuk.
 

Megjegyzések. 1. Könnyen látható (1. ábra), hogy ABC▵∼FGH▵. A megfelelő szakaszok arányát h-val jelölve AB=h⋅GH, AC=h⋅FH, BC=AD=h⋅FG. Ezeket (5)-be beírva és h-val egyszerűsítve az AFGH húrnégyszögre a következő összefüggést kapjuk:
AF⋅GH+FG⋅HA=AG⋅FH,
vagyis húrnégyszögben a szemközti oldalpárok szorzatainak az összege az átlók szorzatával egyenlő. Ez az összefüggés PTOLEMAIOS tétele néven ismeretes. A fenti hasonlóság felhasználásával természetesen ebből a feladat állítása is könnyen következik. Ha viszont az I. alatti bizonyításban az ACD és CAB háromszög helyébe egyaránt az FHG háromszöget tesszük, akkor közvetlen bizonyítást kapunk PTOLEMAIOS tételére.
 

2. A versenyen a bíráló bizottság megelégedett az I. eset tárgyalásával.