Feladat: 1964. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1964/december, 196 - 197. oldal  PDF  |  MathML 
Témakör(ök): Mozgással kapcsolatos szöveges feladatok, Arany Dániel
Hivatkozás(ok):Feladatok: 1964/december: 1964. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Célszerű a szögmérés egységéül az óra számlapjának percbeosztását, azaz a teljes körülfordulás 60-adrészét választani.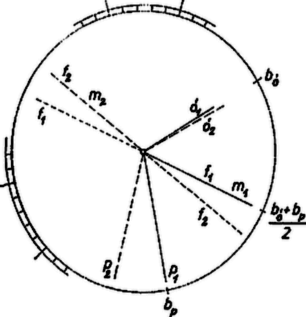
Két mutató az óra számlapját két körcikkre osztja, ezeket ugyanannak az egyenesnek a tengelyből induló két félegyenese felezi. Az óramutatók fedése esetén az egyik körcikk a teljes körlemezbe, a másik a kör egy sugarába megy át; ennek az egyenese tekinthető ilyenkor a szögfelezőnek.
Egy a feltételeket kielégítő H1 helyzetből kiindulva határozzuk meg azt az időtartamot (másodpercben mérve), ami alatt a legközelebbi megfelelő H2 helyzetbe jutnak a mutatók. A másodpercmutató t másodperc alatt t beosztással mozdul el; a H2 helyzetben a szögfelezőnek a másik félegyenesével kerül fedésbe, mint a H1 helyzetben. Tekintetbe kell vennünk azt is, hogy időközben a szögfelező helyzete is megváltozott. Azt az ívet vizsgálva, amelyik az óramutatótól a mutatók járása irányában a percmutató felé terjed, t másodperc alatt az óramutató 560⋅60⋅t=t720 beosztást halad előre, a percmutató t60 beosztást.

 
 
4. ábra
 

Ha a H1 helyzetben az óramutató a b0 beosztásnál, a percmutató pedig bp-nél volt, akkor a szögfelező helyzete (b0+bp)/2 volt, t másodperc múlva pedig (b0+t/720+bp+t/60)/2=(b0+bp)/2+13t/1440, tehát a szögfelező 13t/1440 beosztással jutott tovább.1 Azt, hogy i idő elteltével a másodpercmutató a szögfelezőnek a H1 helyzetben fedett félegyenesével ellentétes irányú félegyenesével került fedésbe, az
i=13i1440+30
egyenlet fejezi ki. Innen i=14401427⋅30=30+3901427mp. Ez nem tartalmazza a H1 helyzetet jellemző adatokat, így azt nyertük, hogy bármely két egymásutáni, a feltételeket kielégítő helyzet közt a nyert i idő telik el.
A három mutatónak 0 óra 0 perc 0 másodperckor elfoglalt helyzete kielégíti a követelményt, tehát az összes megfelelő időpontok i többszörösei:
t=k⋅(30+3901427)mp==43200k1427mp=720k1427perc,


ahol k egész szám. Ha k=1427, akkor t=720perc=12óra. És ettől kezdve ismétlődnek a mutatóállások; k=0,1,2,...,1426 értékekhez viszont csupa különböző mutató-állások tartoznak, hiszen az óramutató egyszer jár körbe, tehát biztosan mindig más helyzetben van.
 
II. megoldás. Azt az időt, ami két egymás utáni megfelelő helyzet közt telik el, kiszámíthatjuk a következő módon is: Az olyan helyzetek időpontjait keressük, amelyekben a szögfelező egyenese és a másodpercmutató egyenese fedi egymást. Ez 12 óra alatt annyiszor következik be, amennyivel többször kerül az utóbbi kiindulási helyzetébe, mint az előbbi, tekintettel arra, hogy a 12 óra végén mindkét egyenes éppen közös kiindulási helyzetébe tér vissza.
A másodpercmutató egyenese félpercenként kerül vissza eredeti helyzetébe, tehát 12 óra alatt 12⋅60⋅2=1440-szer. A szögfelező egyenese, mint láttuk, 13/1440 beosztást halad előre másodpercenként, tehát 12 óra alatt 12⋅60⋅60⋅13/1440=30⋅13 beosztásnyi utat tesz meg. Ez alatt 13-szor kerül fedésbe eredeti helyzetével, miután ez 30 beosztásnyi elforduláskor következik be. A másodpercmutató egyenese tehát 12 óra alatt 1440-13=1427-szer találkozik a szögfelező egyenesével, s így két egymás utáni találkozás közt 12⋅60⋅60/1427=30+390/1427 másodperc telik el.
1A 4. ábra az elfordulásokat nagyítva tünteti fel.