Feladat:	1964. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1964/december, 194 - 195. oldal		PDF  |  MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Középvonal, Háromszögek hasonlósága, Szögfelező egyenes, Pitagorasz-tétel alkalmazásai, Arany Dániel
Hivatkozás(ok):	Feladatok: 1964/december: 1964. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.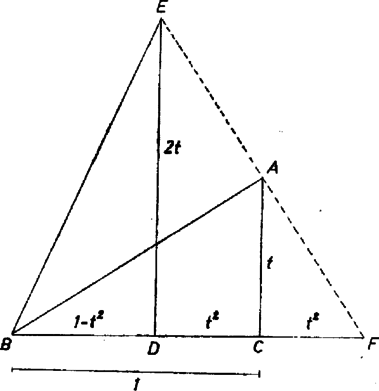     1. ábra   I. megoldás. Rajzoljunk $C$-nél derékszögű háromszöget $AC=t$, $BC=1$ hosszúságú befogókkal; mérjük rá a $BC$ befogóra a $BD=1-t^2$ hosszúságot, majd a $D$-ben a $BC$ egyenesre emelt merőlegesre az egyenes $A$-t tartalmazó oldalán a $DE=2t$ hosszúságot. Ekkor azt kell bebizonyítanunk, hogy $EBD\sphericalangle =2ABC\sphericalangle$, vagyis hogy $AB$ felezi az $EBD$ szöget. Ez következik abból, ha megmutatjuk, hogy az $EA$ egyenes az $EBD$ szögtartományból egyenlő szárú háromszöget vág le, amelynek $AB$ a szimmetriatengelye. Jelöljük az $EA$ és $BD$ egyenes metszéspontját $F$-fel. $AC$ az $FED$ háromszög középvonala, mert párhuzamos $ED$-vel, és fele akkora. Ha ugyanis $A$ és $C$ közelebb, ill. messzebb volna $F$-től, mint a megfelelő oldal felezőpontja, akkor összekötő egyenesük is kisebb, ill. nagyobb volna, mint $ED$ fele. Ezek szerint $EA=AF$, és $FC=CD=CB-DB=1-\left(1-t^2\right)=t^2$. Az $FAC$ és $ABC$ háromszögek hasonlók, mert mindkettő $C$-nél derékszögű, és a befogók aránya egyenlő: $\begin{array}{c}{\displaystyle \frac{AC}{FC}=\frac{t}{t^2}=\frac{1}{t}=\frac{BC}{AC}\mathrm{.}}\end{array}$ A megfelelő befogók egymáshoz képest ugyanolyan irányban ${90}^{\circ }$-kal vannak elforgatva, így ugyanez áll az átfogókra is: $FA\perp AB$. Ezzel beláttuk, hogy $AB$ az $EF$ szakaszt felező és arra merőleges egyenes, tehát az $EBF$ háromszög szimmetriatengelye; így az $EBF\sphericalangle =EBD\sphericalangle$ szögfelezője. 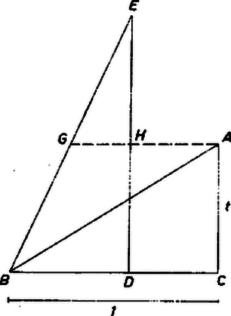  II. megoldás. Rajzoljuk meg az $ABC$ és $EBD$ háromszögeket ugyanúgy, mint az előző megoldásban. Messe az $A$-n át $BC$-vel párhuzamosan húzott egyenes $BE$-t és $DE$-t $G$-ben és $H$-ban. $GH$ a $BDE$ háromszög középvonala, mert $DH=CA=t=\frac{1}{2}DE$, és $GH\Vert BD$, tudjuk továbbá, hogy a középvonal is párhuzamos $BD$-vel, és $H$-n át csak egy ilyen párhuzamos húzható. Így egyrészt Pythagorász tétele szerint (2. ábra)     2. ábra   $\begin{array}{c}{\displaystyle BG=\frac{1}{2}BE=\frac{1}{2}\sqrt[]{B{D}^2+D{E}^2}=\frac{1}{2}\sqrt[]{{\left(1-t^2\right)}^2+4t^2}=\frac{1+t^2}{2}\mathrm{,}}\end{array}$ másrészt $\begin{array}{c}{\displaystyle GA=GH+HA=\frac{BD}{2}+DC=\frac{1-t^2}{2}+\left[1-\left(1-t^2\right)\right]=\frac{1+t^2}{2}\mathrm{.}}\end{array}$ Eszerint az $ABG$ háromszög egyenlő szárú, így ‐ felhasználva azt is, hogy $GA\Vert BC$ ‐ $\begin{array}{c}{\displaystyle EBA\sphericalangle =GBA\sphericalangle =GAB\sphericalangle =ABD\sphericalangle \mathrm{,}}\end{array}$ tehát $EBD\sphericalangle =2ABD\sphericalangle$, és ezt kellett bizonyítanunk. (Tulajdonképpen azt bizonyítottuk, hogy a $G$ közepű $\left(1+t^2\right)/2$ sugarú kör $A$ pontjában érinti $AC$-t, tehát $A$ az érintővel párhuzamos húrhoz tartozó $ED$ ív felezőpontja.)   III. megoldás. Ismét az előző megoldásban látott módon helyezzük el a két háromszöget. Jelöljük $AB$ és $DE$ metszéspontját $M$-mel. Elég megmutatnunk, hogy $M$ ugyanolyan arányú két részre osztja $DE$-t, mint a szögfelező, ugyanis ha egy $P$ pont a $DE$ szakaszon $D$-től $E$ felé mozog, akkor a $DP/PE$ arány számlálója nő, nevezője csökken, és így a tört értéke állandóan nő, egy értéket csak egyszer vesz fel. Tudjuk, hogy a szögfelezőre nézve a szóban forgó osztásarány megegyezik a $BD/BE$ aránnyal, mivel pedig 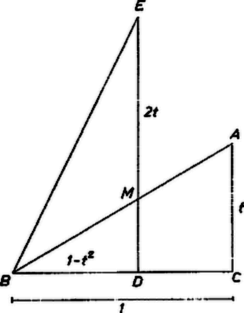$\begin{array}{c}{\displaystyle BE=\sqrt[]{B{D}^2+D{E}^2}=\sqrt[]{{\left(1-t^2\right)}^2+{\left(2t\right)}^2}=1+t^2\mathrm{,}}\end{array}$ így a szögfelező által kimetszett szeletek aránya $\left(1-t^2\right)/\left(1+t^2\right)$.     3. ábra   Az $ABC$ és $MBD$ háromszögek hasonlók, így befogóik arányára: $\begin{array}{c}{\displaystyle \frac{MD}{BD}=\frac{AC}{BC}\mathrm{,}MD=\frac{AC\cdot BD}{BC}=t\left(1-t^2\right)\mathrm{.}}\end{array}$ Ezt felhasználva nyerjük, hogy $\begin{array}{c}{\displaystyle \frac{DM}{ME}=\frac{t\left(1-t^2\right)}{2t-t\left(1-t^2\right)}=\frac{t\left(1-t^2\right)}{t\left(1+t^2\right)}=\frac{BD}{BE}\mathrm{.}}\end{array}$ Az $M$ pont tehát ugyanolyan arányú részekre osztja $DE$-t, mint a szögfelező, és ezzel beláttuk, hogy $BM$ azonos az $EBD$ szög felező egyenesével.