Feladat: 1964. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1964/november, 116 - 117. oldal  PDF  |  MathML 
Témakör(ök): Terület, felszín, Síkgeometriai számítások trigonometria nélkül, Arany Dániel
Hivatkozás(ok):Feladatok: 1964/november: 1964. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az első idom területét úgy kaphatjuk meg a hatszög területéből, hogy hozzáadjuk a kinyúló hat félkör ‐ azaz három kör ‐ területét, és elvesszük a befelé rajzolt hat ugyanakkora sugarú harmadkör ‐ azaz két kör ‐ területét (1. ábra). Így a hatszöget egy kör területével növeltük.
A második idom területe hat kétharmad kör ‐ azaz négy kör ‐ területének hozzáadásával és hat ugyanilyen sugarú félkör ‐ azaz három kör ‐ területének elhagyásával keletkezik a hatszög területéből (2. ábra). Tehát a hatszög területénél ugyancsak egy olyan kör területével nagyobb, amelyiknek sugara a hatszög oldalának a negyede. Így a két idom területe egyenlő.

 

Megjegyzés. Könnyű belátni, hogy a feladat eljárását 6-szög helyett akárhány oldalú szabályos sokszögre végezve mindkét idom területe továbbra is egy kör területével növekszik. (Háromszög esetén a második módon egy négy részre széteső idomot kapunk, 3. ábra.)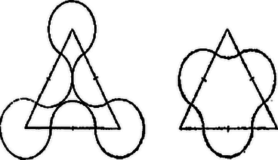
 
 
3. ábra
 

Még általánosabban, ha tetszés szerinti (önmagát nem metsző) sokszöget veszünk 2 példányban, és az egyik oldalainak középpontjai körül kifelé, a másikéi körül befelé rajzolunk egyenlő sugárral félköröket, továbbá ugyanezzel a sugárral az előbbi csúcsai köré befelé, az utóbbié köré kifelé rajzolunk köríveket oldaltól oldalig, a kör sugarát úgy választva, hogy a rajzolt körívek ne nyúljanak egymásba, akkor a két módosított idom területe egyenlő (4. ábra).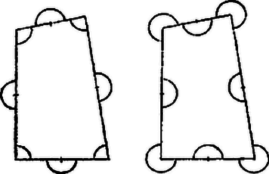
 
 
4. ábra
 

Valóban, legyen a sokszög oldalszáma n, egy kör területe t, a csúcsok köré befelé rajzolt körcikkek területeinek összege B, a külső körcikkeké K, akkor nyilván B+K=nt. Az első idom területét n⋅t2-B-vel változtattuk meg, a másodikét pedig
K-n⋅t2=(nt-B)-n⋅t2=n⋅t2-B
-vel, tehát ugyanannyival, és ezt akartuk belátni. Könnyen igazolható az is, hogy mindig egy kör területével növekedik a sokszög területe.