Kezdőlap


Feladat:	1963. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1964/január, 4 - 5. oldal		PDF \| MathML
Témakör(ök):	Harmadfokú (és arra visszavezethető) egyenletrendszerek, Polinomok szorzattá alakítása, Arany Dániel
Hivatkozás(ok):	Feladatok: 1963/szeptember: 1963. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alkalmas új ismeretlenek bevezetése útján feladatunkat egyszerűbb egyenletekből álló egyenletrendszer megoldására vezethetjük vissza. Legyen pl.

\begin{matrix} x - y = u, és x y = v, \end{matrix}

akkor egyenleteink így alakulnak át:

\begin{matrix} x^{2} - x y + y^{2} = {(x - y)}^{2} + x y = u^{2} + v = 2, & (1a) \\ x^{3} - y^{3} = {(x - y)}^{3} + 3 x y (x - y) = u^{3} + 3 u v = 4. & (2a) \end{matrix}

Az első egyenletből

v

kifejezését a másodikba helyettesítve:

\begin{matrix} u^{3} + 3 u (2 - u^{2}) = 4. \end{matrix}

Rendezés és egyszerűsítés után a bal oldalt szorzattá alakíthatjuk:

\begin{matrix} u^{3} - 3 u + 2 = 0, \\ (u^{3} - u) - 2 (u - 1) = (u - 1) [u (u + 1) - 2] = (u - 1) (u^{2} + u - 2) . \end{matrix}

Ez a szorzat akkor és csak akkor 0, ha valamelyik tényezője 0, tehát vagy

u - 1 = 0

u_{1} = 1

, vagy

u^{2} + u - 2 = 0

. Az utóbbi egyenlet két gyöke

u_{2} = 1

és

u_{3} = - 2

. Az

u

-khoz tartozó

v

-ket az (1a) egyenletből számíthatjuk ki,

\begin{matrix} v_{1} = 1, v_{2} = 1, v_{3} = - 2. \end{matrix}

u_{1} = 1

v_{1} = 1

gyökrendszerhez tartozó

x

és

y

értékeket az

\begin{matrix} u = x - y = 1, v = x y = 1 \end{matrix}

egyenletekből kiszámítva

\begin{matrix} x_{1} = \frac{\sqrt[]{5} + 1}{2}, y_{1} = \frac{\sqrt[]{5} - 1}{2}; \\ x_{2} = - \frac{\sqrt[]{5} - 1}{2}, y_{2} = - \frac{\sqrt[]{5} + 1}{2} . \end{matrix}

u_{2}

v_{2}

gyökpárból nem kapunk új megoldást. Az

u_{3} = - 2

v_{3} = - 2

gyökpárral adódó

x - y = - 2

x y = - 2

egyenletrendszernek nincs valós megoldása.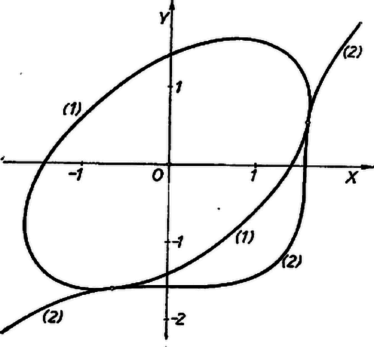

Megjegyzés. Bizonyítás nélkül megemlítjük, hogy (1) képe a derékszögű koordinátarendszerben olyan ellipszis, amelynek középpontja az origó, szimmetria tengelyei a koordináta‐tengelyekkel

45^{\circ}

-os szöget zárnak be, nagy tengelye az I. és III. síknegyedekben halad, ‐ (2) képe pedig egy ún. harmadrendű görbe. A mindkét egyenletet kielégítő

x

y

számpárokhoz tartozó pontok a görbéknek közös pontjai, ez esetben érintkezési pontok, bennük a két görbének közös az érintője is.