Kezdőlap


Feladat:	1963. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1963/november, 107 - 108. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Pitagorasz-tétel alkalmazásai, Pont körüli forgatás, Arany Dániel
Hivatkozás(ok):	Feladatok: 1963/november: 1963. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Elég megmutatni, hogy a megfelelő összefüggés fennáll a szóban forgó szakaszoknak az $O A$ egyenesen levő vetületére. Ugyanis mindegyik vetület ugyanannyiad része (esetünkben $1 / \sqrt[]{2}$ -szöröse) az eredeti szakasznak, és így a szakaszokat a vetületekkel helyettesítve (1) mindkét oldala ugyanazzal, a mondott arány négyzetével szorzódik.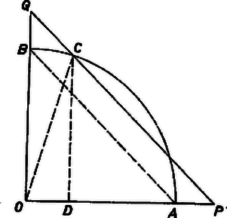

1. ábra

A B

C P

C Q

szakaszok vetülete

A O = r

, (a kör sugara),

D P

és

D O

, továbbá, mivel a

C D P

háromszög egyenlő szárú, így

D P = D C

, tehát a vetületekre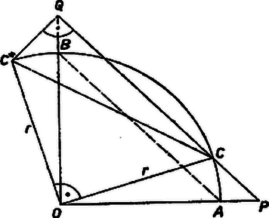

\begin{matrix} D P^{2} + D O^{2} = D C^{2} + D O^{2} = O C^{2} = r^{2} = O A^{2}, \end{matrix}

mivel a

C D O

háromszög derékszögű. Fennáll tehát a bizonyítandó összefüggés is.

II. megoldás. Forgassuk el a kör középpontja körül a

Q P

szakaszt a

C

ponttal együtt

90^{\circ}

-kal úgy, hogy a

P

pont a

Q

pontba kerüljön, és az elforgatott

C

pontot jelöljük

C^{*}

-gal. Ekkor a

C^{*} C Q

háromszög

Q

-nál fekvő szöge derékszög, és

Q C^{*} = P C

. Másrészt a

C^{*} O C ∢ = 90^{\circ}

, így

C^{*} C = r \sqrt[]{2}

. Eszerint az (1) összefüggés éppen a

C^{*} C Q

derékszögű háromszögre felírt Pythagoras-tétel.

2. ábra

Megjegyzés. Állításunk akkor is érvényes, ha megrajzolva a teljes

O

középpontú,

r

sugarú kört, az

A B

-vel párhuzamos szelő ezt a negyedkörön kívül eső

C

pontban metszi. Mindkét előbbi megoldás alkalmas ennek bebizonyítására is.