Kezdőlap


Feladat:	1962. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1963/január, 11 - 16. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Középpontos tükrözés, Trapézok, Arany Dániel
Hivatkozás(ok):	Feladatok: 1962/szeptember: 1962. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2. feladat. Bizonyítsuk be, hogy ha két hatszög oldalainak felezőpontjai rendre megegyeznek, akkor a két hatszög területe egyenlő.

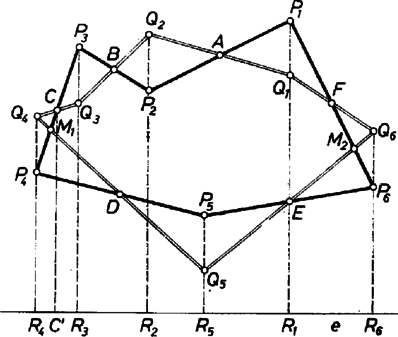
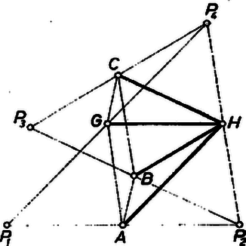
I. megoldás. Legyen a

P_{1} P_{2} P_{3} P_{4} P_{5} P_{6} = P

hatszög

P_{1} P_{2}

P_{2} P_{3}

...

P_{6} P_{1}

oldalának felezőpontja rendre

A

B

C

D

E

F

, és tegyük fel, hogy rendre ugyanezen pontok felezik a

Q_{1} Q_{2} Q_{3} Q_{4} Q_{5} Q_{6} = Q

hatszög egymás utáni

Q_{1} Q_{2}

Q_{2} Q_{3}

...

Q_{6} Q_{1}

oldalát is. Azt kell bebizonyítanunk, hogy a

P

és

Q

hatszögek területe egyenlő.
Egyelőre feltesszük, hogy sem

P

, sem

Q

nem hurkolt idom és meggondolásainkat az 1. ábra esetéhez kapcsoljuk hozzá. A közös felezőpontokban a két hatszög egy-egy oldala metszi egymást, pl.

A

-ban a

P_{1} P_{2}

és

Q_{1} Q_{2}

oldalak. Ezért az egyik hatszög kerületén végighaladva mindegyik felezőpontban átlépjük a másik hatszög kerületét, vagy belépünk abba, vagy kilépünk belőle, ‐ hacsaknem kivételesen

P

és

Q

egy-egy oldalegyenese egybeesik, és így egy szakaszon közös határukon haladunk. Ennélfogva

Q

területének is bizonyos részei

P

-n belül vannak, más részei

P

-n kívül és viszont. Pl. az

A P_{1} Q_{1}

háromszög

P

-höz hozzátartozik,

Q

-hoz pedig kívülről csatlakozik, az

A P_{2} Q_{2}

háromszög viszont

Q

-n belül, egyszersmind

P

-n kívül van. E két háromszög egybevágó, mert

A

-ból kiinduló oldalaik páronként egyenlők és a köztük levő szögek csúcsszögek, ezért területük is egyenlő. Így kapjuk a következő 6 egyenlőséget (a háromszögek területét ugyanúgy jelölve, ahogy magukat a háromszögeket szokás):

\begin{matrix} A P_{1} Q_{1} = A P_{2} Q_{2}, \\ B P_{3} Q_{3} = B P_{2} Q_{2}, \\ C P_{3} Q_{3} = C P_{4} Q_{4}, & (7) \\ D P_{4} Q_{4} = D P_{5} Q_{5}, \\ E P_{6} Q_{6} = E P_{5} Q_{5}, \\ F P_{1} Q_{1} = F P_{6} Q_{6} . \end{matrix}

\begin{matrix} 1. ábra \end{matrix}

A balról felsorolt háromszögek mind kívülről csatlakoznak

Q

-hoz, a jobboldaliak pedig

P

-hez. Ezért

Q

-hoz hozzávéve a bal oldali háromszögeket, az

A Q_{2} B P_{3} C Q_{4} P_{4} D Q_{5} E P_{6} Q_{6} F P_{1} = S

sokszöget kapjuk. Ugyanezt a sokszöget kapjuk

P

-ből a jobb oldalon felsorolt háromszögek hozzávételével. Eszerint, a

P

Q

S

idom területét is

P

-vel,

Q

-val, ill.

S

-sel jelölve, a (7) egyenlőségek összeadásával adódó egyenlőség két oldalának értékét pedig

T

-vel, a következő egyenlőséget írhatjuk fel:

\begin{matrix} S = Q + T = P + T . \end{matrix}

Innen

Q = P

. Ezzel az állítást ‐ az ábrán felvett esetre ‐ bebizonyítottuk.

Megjegyzés. Számos versenyző a

P

és

Q

hatszögek közös részéhez, a

Q_{1} A P_{2} B Q_{3} C M_{1} D P_{5} E M_{2} F

sokszöghöz vette hozzá a bal-, ill. jobboldalon álló háromszögeket. (

M_{1}

P_{3} P_{4}

és

Q_{4} Q_{5}

M_{2}

pedig a

P P_{1}

és

Q_{5} Q_{6}

oldalak közös pontja; ezek nem egymásnak megfelelő oldalak; csak esetleges, hogy van közös pontjuk; ábránkon több ilyen oldalpár nincs is.) Egy részük nem vette észre, hogy így nem

P

-t, ill.

Q

-t kapta, hanem nagyobb idomot, mert egy-egy hozzávett háromszög részei, az

M_{1} P_{4} Q_{4}

és

M_{2} P_{6} Q_{6}

háromszögek sem

P

-hez, sem

Q

-hoz nem tartoznak hozzá. Mások ezek elvételével tették teljessé bizonyításukat.
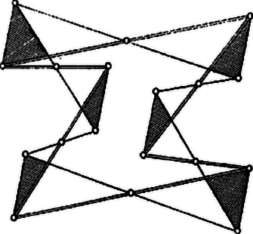
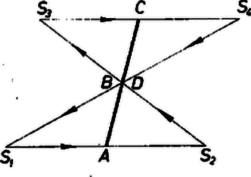
A (7) háromszögekkel ,,kétszer fedett''

M_{1} P_{4} Q_{4}

háromszög azért keletkezett, mert a

C

D

egymás utáni felezőpontok a

P_{4} Q_{4}

egyenes ugyanazon oldalán vannak. Ha egy ilyen

P_{i} Q_{i}

egyenes átmegy a

P_{i - 1} P_{i}

, vagy a

P_{i} P_{i + 1}

oldal felezőpontján, akkor a (7) felsorolás megfelelő háromszöge egyenesszakasszá fajul, egyszersmind kétszer fedett háromszög sem keletkezik. Előfordulhat viszont, hogy mind a hat szakaszon létrejön kétszer fedett háromszög (2. ábra).

\begin{matrix} 2. ábra \end{matrix}

II. megoldás.

P

és

Q

egy-egy közös felezőponttal bíró oldalának ‐ pl. az egymást

A

-ban felező

P_{1} P_{2}

Q_{1} Q_{2}

oldalpárnak ‐ végpontjai paralelogrammát alkotnak, ezért

P_{1} Q_{1} ∥ Q_{2} P_{2} ∥ P_{3} Q_{3} ∥ Q_{4} P_{4} ∥ P_{5} Q_{5} ∥ Q_{6} P_{6}

. Vegyünk egy a

P_{1} Q_{1}

-re merőleges, sem

P

-t, sem

Q

-t nem metsző

e

egyenest, és vetítsük erre

P

és

Q

csúcsait. A

P_{1}, Q_{1}

, a

P_{2}, Q_{2}, ...

, a

P_{6}, Q_{6}

pontpárok vetülete egybeesik, jelöljük ezeket rendre

R_{1}, R_{2}, ..., R_{6}

-tal (1. ábra, ezek közül egyesek egybe is eshetnek). Ekkor

P

és

Q

területét úgy kaphatjuk, hogy 4 ‐ 4 trapéz területének összegéből kivonjuk más 2 ‐ 2 trapéz területének összegét:

\begin{matrix} P = P_{4} P_{3} R_{3} R_{4} + P_{3} P_{2} R_{2} R_{3} + P_{2} P_{1} R_{1} R_{2} + P_{1} P_{6} R_{6} R_{1} - P_{4} P_{5} R_{5} R_{4} - P_{5} P_{6} R_{6} R_{5}, & (8) \\ Q = Q_{4} Q_{3} R_{3} R_{4} + Q_{3} Q_{2} R_{2} R_{3} + Q_{2} Q_{1} R_{1} R_{2} + Q_{1} Q_{6} R_{6} R_{1} - Q_{4} Q_{5} R_{5} R_{4} - Q_{5} Q_{6} R_{6} R_{5} . \end{matrix}

A két kifejezés ugyanazon sorszámú tagjai páronként egyenlők, mert a megfelelő trapézok magassága és középvonala közös; pl. az első tagokra

R_{4} R_{3}

és

C C'

, ahol

C'

C

-nek

e

-n levő vetülete. Ezért

P = Q

.
Az ábránkétól különböző esetekben a (8) előállításokban a hozzáadandó tagok száma legalább 1, legfeljebb 5, és ezt a számot a levonandó tagok száma 6-ra egészíti ki. Amennyiben szomszédos indexű

R

pontok egybeesnek, a tagok száma csökken.

Megjegyzések. 1. A most bemutatott módon szokás meghatározni sokszögek területét, ha csúcsaik koordinátáikkal vannak adva. Így határozza meg a földmérő mérnök is sokszög alakú telkek területét.

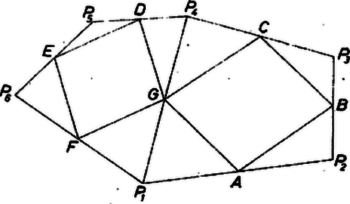
3. ábra

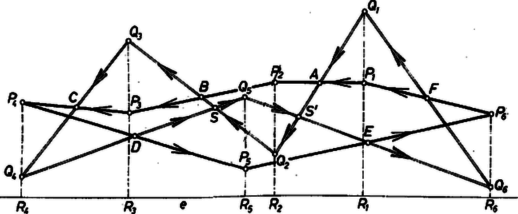
2. Ez a bizonyítás mutatja, hogy az állítás a 3. ábra esetében is érvényes, ahol

P

és

Q

közös része nem összefüggő: két négyszögre és egy hatszögre esik szét. Ebben az esetben az I. megoldás megjegyzésében említett meggondolást jelentősen ki kellene egészítenünk.

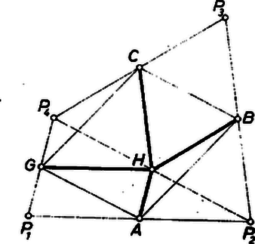
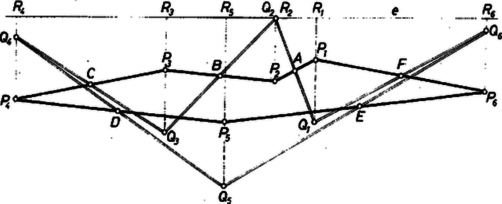
3. A 4. ábra esetében

Q

hurkolt,

Q_{2} Q_{3}

és

Q_{4} Q_{5}

oldalszakaszainak közös pontja

S

, a

Q_{1} Q_{2}

és

Q_{5} Q_{6}

szakaszok közös pontja

S'

. Ilyen idom területét eddig nem értelmeztük. Az oldalszakaszok, ill. részeik a

Q_{1} S' Q_{6} = H_{1}

és

S Q_{3} Q_{4} = H_{2}

háromszögeket és az

S'_{1} Q_{2} S Q_{5} = N

négyszöget határolják körül.

\begin{matrix} 4. ábra \end{matrix}

Nézzük meg, mit ad ebben az esetben a II. megoldás gondolatmenete.

N

területét (8) pozitív tagjaiban nem vettük számításba, mert a négyszög az

R_{3} Q_{3} Q_{2} R_{2}

R_{2} Q_{2} Q_{1} R_{1}

trapézokon kívül van, a negatív tagokban viszont levontuk, mert az

R_{4} Q_{4} Q_{5} R_{5}

R_{5} Q_{5} Q_{6} R_{6}

trapézok tartalmazzák. Eszerint az állítás érvényes marad, ha

Q

területén ezúttal a

H_{1} + H_{2} - N

kifejezést értjük. (Könnyen megjegyezhető ez a megállapodás, ha összehasonlítjuk a

H_{1}

H_{2}

és

N

részek körüljárásának irányát, miközben

Q

kerületét

Q_{1}

Q_{2}

Q_{3}

Q_{4}

Q_{5}

Q_{6}

sorrendben körüljárjuk.

H_{1}

és

H_{2}

körüljárása az óramutató járásával ellentétes irányú, akárcsak a

P = P_{1} P_{2} P_{3} P_{4} P_{5} P_{6}

körüljárásé,

N

körüljárása pedig az óra járásával megegyező. Másképpen:

H_{1}

H_{2}

és

P

körülhatárolt része a mondott körüljárásban a menetvonal bal oldalán van,

N

-é pedig a jobb oldalon.)

III. megoldás. Ismeretes, hogy bármely négyszög oldalfelező pontjai egy paralelogramma csúcsai, melynek oldalai párhuzamosak a négyszög átlóival és fele akkorák, mint az átlók (5. ábra,

P_{1} P_{2} P_{3} P_{4}

és

A B C G

). Megmutatjuk, hogy a paralelogramma területe fele a

P_{1} P_{2} P_{3} P_{4}

négyszög területének. Valóban, a

P_{2} P_{4}

átló

H

felezőpontját

A

-val,

B

-vel,

C

-vel, ill.

G

-vel összekötő szakasz rendre párhuzamos és egyenlő a

P_{4} P_{1}

P_{4} P_{3}

P_{2} P_{3}

, ill.

P_{2} P_{1}

oldal felezésével előállt szakaszokkal. Ezért az

A B H

és

C G H

háromszögek áttolhatók

G C P_{4}

-be, ill.

B A P_{2}

-be és a

B C H

és

G A H

háromszögek

180^{\circ}

-os forgatással átforgathatók

C B P_{3}

-ba, ill.

A G P_{1}

-be. Így pedig a négy részre darabolt

A B C G

paralelogramma részeivel maradéktalanul lefedhetjük a

P_{1} P_{2} P_{3} P_{4}

négyszögnek a paralelogrammán kívüli részeit.

\begin{matrix} 5. ábra \end{matrix}

\begin{matrix} 6. ábra \end{matrix}

(Állításunk hurkolt négyszögre is igaz ‐ 6. ábra ‐, ha ennek területét a fenti megjegyzés szerint értelmezzük, továbbá a felhasznált háromszögek területét pozitív, ill. negatív előjellel tekintjük aszerint, hogy felsorolt körüljárásuk iránya megegyező, ill. ellentétes az

A B C G

paralelogramma körüljárásának irányával. Ha a hurkolt négyszöget az

S_{1} S_{2} S_{3} S_{4}

paralelogrammából képezzük az

S_{3}

és

S_{4}

csúcsok felcserélésével, akkor az oldalfelező pontok egy egyenesre esnek (7. ábra),

A B C D = 0

, megfelelően annak, hogy

S_{1} S_{2} B △ ≅ S_{4} S_{3} D △

, és így különbségük 0. A továbbiakban is minden területet így értünk.)

\begin{matrix} 7. ábra \end{matrix}

\begin{matrix} 8. ábra \end{matrix}

Ezek szerint a fenti

P

hatszöget a

P_{1} P_{4}

átlóval a

P_{1} P_{2} P_{3} P_{4}

és

P_{1} P_{4} P_{5} P_{6}

négyszögekre bontva és ezen átló felezőpontját

G

-vel jelölve

P

területe kétszerese az

A B C G

és

G D E F

paralelogrammák területe összegének (8. ábra).
Ha mármost

Q

hatszög oldalainak felező pontjai ugyancsak rendre az

A

B

...

F

pontok, akkor

Q

területe is kétszerese az

A B C G + D E F G

összegnek, és így egyenlő

P

területével, ugyanis a paralelogrammák negyedik (

G

) csúcsát az első három csúcs egyértelműen meghatározza, ha sorrendjük is adva van. Ezzel az állítást bebizonyítottuk.

Megjegyzések. 1. Látható, hogy a négyszögoldalak felezőpontjai közül csak 3 független egymástól (

A

B

C

) és sorrendjük meghatározza

G

-t. Másrészt az is, hogy tetszés szerinti számú olyan négyszög szerkeszthető, melyre az oldalak felezőpontjai rendre azonosak

A

B

C

G

-vel. Ha ugyanis egy tetszés szerinti

S_{1}

pont

A

-ra vett tükörképe

S_{2}

S_{2}

-é

B

-re

S_{3}

és

S_{3}

-é

C

-re

S_{4}

, akkor

S_{4}

-nek

G

-re vett tükörképe azonos

S_{1}

-gyel. Hasonlóan a hatszögoldalak felezőpontjai közül csak öt független egymástól. Pl. felvéve az

A

B

C

D

és

E

pontokat, megszerkeszthetjük a

G

pontot, mint az

A B C G

paralelogramma negyedik csúcsát, majd az

F

pontot, mint a

G D E F

paralelogramma negyedik csúcsát. Ha viszont az adott 6 felezőpont megfelel e feltételnek, akkor az előbbihez hasonló tükrözéssorozattal akárhány olyan hatszög szerkeszthető, melyre az egymás utáni oldalak felezőpontja

A

B

C

D

E

F

.
2. Az eddigi felezőpontokat

A

B

C

F

E

D

sorrendben véve a létrejövő hatszögek területe az előbbiekétől általában különböző, mert így a

D E F G

paralelogramma helyére

F E D G

lép, és ezek területei egymásnak negatívjai. Ezért nem felesleges a feladatnak az a kikötése, hogy a hatszögoldalak felezőpontjainak rendre kell megegyezniök.
3. Az állítás hatszög helyett bármely páros oldalszámú sokszög esetére érvényes, megjegyezve azt, hogy az utolsó felezőpontot a többiek ‐ és sorrendjük ‐ egyértelműen meghatározzák. Ez abból következik, hogy minden

2 n

oldalú sokszög (

2 n \geq 6

) egy csúcsból kiinduló átlókkal

n - 1

négyszögre bontható.
Néhány versenyző akárhány oldalú sokszögre érvényesnek vélte az állítást. Ez a sejtés a páratlan oldalszámú sokszögekre semmitmondó. Ugyanis egy háromszög oldalainak felezőpontjai egyértelműen meghatározzák a háromszöget, és ugyanez áll a

2 n - 1

oldalú sokszögekre^{$^{*}$} (

2 n - 1 \geq 5

), mert ezekben egy csúcsból azokat az átlókat meghúzva, amelyek a sokszöget egy négyszögre és egy

2 n - 3

, ill.

2 n - 5, ...

-szögre bontják (pl.

P_{1} P_{4}, P_{1} P_{6}, P_{1} P_{8}, ..., P_{1} P_{2 n - 2}

) utoljára háromszöget kapunk. Ezt az oldalak felezőpontjai egyértelműen meghatározzák és ebből kiindulva a sokszög többi csúcsai is egyértelműen meghatározhatók.

^{$^{*}$}Lásd 502. gyakorlat, K. M. L. 18 (1959/2) 45. o. és 557. gyakorlat, K. M. L. 19 (1959/11) 136. o.