Kezdőlap


Feladat:	1962. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1962/november, 105 - 106. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Arany Dániel
Hivatkozás(ok):	Feladatok: 1962/szeptember: 1962. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az oldalak érintésén a szokásnak megfelelően az oldalszakaszok érintését értjük. Így a keresett körök a háromszög belsejében vannak. Nem érintheti két különböző kör, amelyek sugara egyenlő, ugyanazt a két oldalt, így az egyik oldalt mindkét kör érinti, a másik kettőt egy‐egy kör.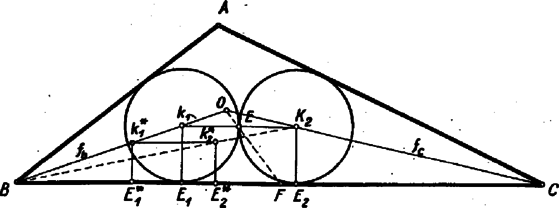
Legyen a két kör középpontja $K_{1}$ és $K_{2}$ , érintsék egymást az $E$ pontban, érintse mindkettő az $A B C$ háromszög $B C$ oldalát, az első az $E_{1}$ , a második az $E_{2}$ pontban. A háromszög $B$ -ből, ill. $C$ -ből induló szögfelezője legyen $f_{b}$ , ill. $f_{c}$ , ezen van a $K_{1}$ , ill. $K_{2}$ középpont; a két szögfelező metszéspontja legyen $O$ .

A követelmény alapján

K_{1} E_{1} # K_{2} E_{2}

, a két szakasz merőleges

B C

-re és

K_{1} K_{2} = 2 K_{1} E = 2 K_{1} E_{1}

. Ezek szerint a

K_{1} E_{1} E_{2} K_{2} = T

négyszög olyan a

B C O

háromszögbe írt téglalap, melyben a

B C

-n levő és a rá merőleges oldalak aránya

2 : 1

.
Ezek szerint

T

-t hasonlósági transzformációval szerkeszthetjük meg, pl. a következőképpen: Legyen

K_{1}^{*}

B O

szakasz egy tetszés szerinti pontja. Bocsássunk

K_{1}^{*}

-ból

K_{1}^{*} E_{1}^{*}

merőlegest

B C

-re és mérjünk

E_{1}^{*}

-ból

2 K_{1}^{*} E_{1}^{*}

hosszúságú szakaszt ‐ legyen ez

E_{1}^{*} E_{2}^{*}

‐ a

B C

egyenesre úgy, hogy az

E_{1}^{*} E_{2}^{*}

irány megegyezzék a

B C

iránnyal, végül egészítsük ki e pontokat egy

K_{1}^{*} E_{1}^{*} E_{2}^{*} K_{2}^{*}

télalappá. Ekkor a

B K_{2}^{*}

egyenesnek

C O

-val való metszéspontja a keresett

K_{2}

, és az ezen át

B C

-vel párhuzamos egyenes

B O

-ból kimetszi

K_{1}

-et.
Valóban, a

K_{2}^{*} E_{1}^{*} K_{1}^{*}

és

K_{2} E_{1} K_{1}

derékszögű háromszögek hasonlók, mert a megfelelő csúcsaikat összekötő egyenesek

B

-ben metszik egymást és két pár megfelelő oldaluk párhuzamos és egyenlő irányú (a befogók), ennélfogva hasonló helyzetűek. Így

\begin{matrix} K_{1} K_{2} : K_{1} E_{1} = K_{1}^{*} K_{2}^{*} : K_{1}^{*} E_{1}^{*} = 2 : 1. \end{matrix}

K_{1}

és

K_{2}

körül

K_{1} E_{1}

sugárral írt körök érintik egymást és a

B C

oldalt, továbbá a

B A

, ill.

C A

oldalt is, mert ezek

B C

-vel tükrös párok

f_{b}

-re, ill.

f_{c}

-re nézve.
A

B K_{2}^{*}

egyenes minden háromszögben metszi

C O

-t, mert

K_{2}^{*}

O B C

konvex szögtérbe esik, tehát a szerkesztés egyértelműen végrehajtható.

B C

helyére a

B A

, majd a

C A

oldalt választva a két kör közös érintője gyanánt ‐ további két, a követelménynek megfelelő körpárt kapunk. Egyenlő szárú háromszögben a 6 kör közül kettő a szimmetria miatt nyilván azonos, azok, amelyek a két szárat érintik, amikor közös érintőnek az egyik szárat vesszük. Egyenlő oldalú háromszögből kiindulva pedig összesen 3 kör adódik.

Megjegyzések. 1. A hasonlósági transzformációt sok másféleképpen is felhasználták a versenyzők. Pl. a

B C

oldalt és egymást is érintő két egyenlő sugarú körhöz szerkesztettek

A B

-vel, ill.

A C

-vel párhuzamos érintőt úgy, hogy a keletkezett háromszög a köröket tartalmazza; vagy a

B C

szakaszra mint hosszabb oldalra kifelé szerkesztettek

T

-hez hasonló téglalapot, ennek

B C

-vel párhuzamos oldala

f_{b}

-vel és

f_{c}

-vel ad az

O B C

-hez hasonló helyzetű háromszöget stb. Ezek a háromszögek azután alkalmas nagyítással vagy kicsinyítéssel átvihetők az adott ábra megfelelő részébe.
2. Észrevehetjük azt is, hogy a

K_{1} K_{2}

szakasz

E

felezőpontja a

B C O

háromszögnek

B C

-hez tartozó súlyvonalán van. Ezért az

O F

súlyvonal által kettéosztott

B C O

háromszögnek egyik felébe négyzetet szerkeszteni: szintén a kitűzött feladattal egyenértékű feladat.