Kezdőlap


Feladat:	1961. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1962/január, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Trapézok, Húrnégyszögek, Pont körüli forgatás, Arany Dániel
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1961. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mérjük rá $a$ és $b$ -re $O$ -tól az állandó $A O + O B$ szakaszt és jelöljük a végpontot $A_{0}$ , ill. $B_{0}$ -lal. $O$ , $A_{0}$ és $B_{0}$ tágabb értelemben hozzátartozik a keresett mértani helyhez. Ha ugyanis $A O = O B = O A_{0} / 2$ , akkor az $A B$ -vel $O$ -n át húzott párhuzamos érinti az $A B$ átmérőjű kört, így $C$ gyanánt csak maga $O$ vehet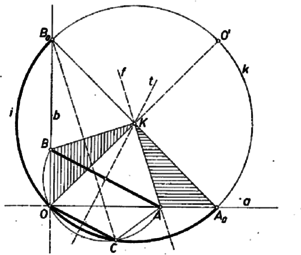ő.

Ha pedig

A

A_{0}

határhelyzetbe, és ezért

B

O

-ba kerül, akkor

A B

átmegy

O

-n, és így

C

egybeesik

A_{0}

-lal. Ugyanígy

A \equiv O

B \equiv B_{0}

esetén

C \equiv B_{0}

. Néhány további

C

-pont megszerkesztése után a szemlélet azt a sejtést adja, hogy a keresett mértani hely az

A_{0} B_{0}

átmérő fölötti,

O

-n átmenő

i

félkör, más szóval az

A_{0} B_{0} O

egyenlő szárú derékszögű háromszög köré írt

k

körnek az

O

-t tartalmazó

A_{0} B_{0} = i

íve. Bebizonyítjuk, hogy

A_{0} B_{0}

felezőpontját

K

-val jelölve mindig fennáll

K C = K A_{0} = K O

.
Szerkesztésünk szerint

B O + O A = O A_{0} = O A + A A_{0}

, tehát

B O = A A_{0}

; másrészt

K O = K A_{0}

és

K O B ∢ = K A_{0} A ∢ = 45^{\circ}

, így a

K O B

és

K A_{0} A

háromszögek egybevágók. Ezért

K B = K A

, vagyis

A B

-nek

t

felező merőlegese az

A B

minden helyzetében átmegy

K

-n. Ámde

t

egyszersmind az

A C O B

húrtrapéz szimmetriatengelye, tehát

O C

-t is merőlegesen felezi, és így valóban

K C = K O = K A_{0}

. Eszerint a mértani hely minden pontja

k

-n van.
Megmutatjuk másrészt, hogy az

i

ív minden

C^{*}

pontja hozzátartozik a keresett mértani helyhez. Messe a

C^{*} A_{0}

húr

f

felező merőlegese

a

-t

A^{*}

-ban, forgassuk el a

K A_{0} A^{*}

háromszöget

K

körül úgy, hogy

A_{0}

O

-ba jusson, és legyen ekkor

A^{*}

új helyzete

B^{*}

. Megmutatjuk, hogy az

A^{*}

B^{*}

pontokhoz a feladat feltételei szerint

C^{*}

tartozik hozzá. ¹
A használt forgatás szöge

A_{0} K O ∢ = 90^{\circ}

, ezért az

a

-n levő

A_{0} A^{*}

oldal új

O B^{*}

helyzete merőleges

a

-ra, tehát

B^{*}

b

-n van. Továbbá

O B^{*} = A_{0} A^{*}

, tehát

O A^{*} + O B^{*} = O A^{*} + A^{*} A_{0} = O A_{0}

, az előírt állandó. ‐ Másrészt

f

átmegy

K

-n, így a

K A^{*} C^{*}

háromszög az

f

-re vett tükörképe

K A^{*} A_{0}

-nak, az utóbbi pedig azonos körüljárással egybevágó

K B^{*} O

-val, tehát

K A^{*} C^{*}

és

K B^{*} O

ellentétes körüljárással egybevágók. És mivel

K

csúcsuk közös, azért van olyan

t^{*}

tengely, amelyre tükrözve egymásba mennek át. Tehát

A^{*} B^{*}

és

C^{*} O

párhuzamosak (merőlegesek

t^{*}

-ra), és az

A^{*} B^{*}

C^{*}

O

pontok egy szimmetrikus trapéz csúcsai. Végül

A^{*} O B^{*} ∢ = 90^{\circ}

, ezért

O

, és vele

C^{*}

is rajta van az

A^{*} B^{*}

átmérőjű körön. Ezzel állításunkat bebizonyítottuk.
Amíg

C

O

-t tartalmazó

A_{0} B_{0} = i

íven van, addig

A_{0} K A ∢ = A_{0} K C ∢ / 2 = A_{0} B_{0} C ∢ < 90^{\circ} = A_{0} K O ∢

, tehát

A

A_{0} O

szakaszon, az

a

félegyenesen van, és ennélfogva

B

b

-nek pontja. Ha viszont

C

-t a

k

-nak az

A_{0} O B_{0}

szögtartományba eső ívén vennénk, akkor a

C O

-val párhuzamos egyenesek vagy csak

a

-t, vagy csak

b

-t metszenék, így nem lehetséges a

C

-t előállító

A

B

pontpár.
Mindezek szerint a

C

pontok mértani helye valóban az

A_{0} O B_{0}

félkörív.

Megjegyzés. Ha megengedjük, hogy

A

túlmehessen az

A_{0}

határhelyzeten, akkor

A O + O B

állandósága csak negatív

O B

-vel maradhat fenn. Ennek a

b

félegyenes

O

-n túli meghosszabbításán levő

B

pontot feleltetve meg, a fentiekhez hasonlóan belátható, hogy

C

mértani helye az

O B_{0}

negyedkörnek

K

-ra vett

O' A_{0}

tükörképe (az

O'

pont kivételével, mert így mindig fennáll

| O B | < O A

, tehát

A B

és

O C

a

-val

45^{\circ}

-nál kisebb szöget zár be). Ha pedig

B

halad túl

B_{0}

-on és

A

a

félegyenes

O

-n túli meghosszabbításán van, akkor

C

mértani helye az

O' B_{0}

negyedív (

O'

-t kizárva). Ezek szerint előjellel vett

O A

O B

távolságokat tekintve

C

mértani helye a

k

kör az

O'

pont kivételével.

¹Az ábrán a *-okat nem tüntettük fel.