Kezdőlap


Feladat:	1961. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1961/november, 100 - 102. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Háromszögek hasonlósága, Thalesz-kör, Arany Dániel
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1961. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $A B C$ derékszögű háromszög $C B$ , $C A$ befogója fölé írt kör $p$ , ill. $q$ , és messe ezeket a $C$ -n átmenő $s$ egyenes másodszor $P$ , $Q$ -ban. $P Q$ mint átfogó fölé a $C B$ , $C A$ -val párhuzamos befogókkal két derékszögű háromszöget szerkeszthetünk, legyenek ezek csúcsai $U$ és $V$ úgy, hogy $P U ∥ C A$ és $Q U ∥ C B$ , ill. $P V ∥ C B$ és $Q V ∥ C A$ . A keresett mértani helyet mindazok és csak azok a pontok alkotják, amelyek akár $U$ , akár $V$ gyanánt fellépnek, mialatt $s$ minden lehetséges helyzetét felveszi, azaz $C$ körül $180^{\circ}$ -kal elfordul.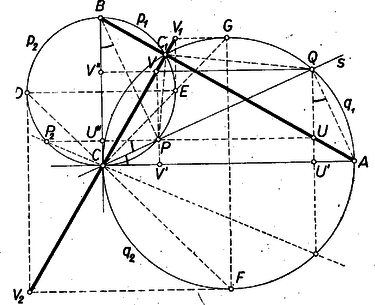

Tekintsük az

U

csúcsok mértani helyét. Néhányukat megszerkesztve mindegyiket az

A B

átfogón kapjuk. Megmutatjuk, hogy az

U

pontok mértani helye az

A B

szakasz. E szakasz meghosszabbításaira nem eshet

U

pont, hiszen a

p

-n fekvő

P

, és vele

U

sem juthat távolabb

C A

-tól, mint

B

és

C A

-nak csak azon az oldalán lehet, mint

B

, továbbá a

q

-n fekvő

Q

-val együtt

U

nem juthat távolabb

C B

-től, mint

A

, a

C B

-nek azon az oldalán van, mint

A

.
Legyen

U

vetülete

C A

-ra,

C B

-re

U'

U''

. Megmutatjuk, hogy

s

helyzetétől függetlenül

U' U : U' A = C B : C A

; ebből következik, hogy

U' A U

és

C A B

derékszögű háromszögek hasonlók, és ebből

U' A U ∢ = C A U ∢ = C A B ∢

, tehát

A U

egyenes egybeesik

A B

-vel. ‐ Thalész tétele szerint

B P

és

A Q

merőlegesek

s

-re, és ezért a

P C U''

B C P

C A Q

Q A U'

derékszögű háromszögek hasonlók, mert megfelelő hegyes szögeik vagy közösek, vagy párhuzamos, vagy merőleges szárúak, és így egyenlők. Másrészt a

C U' U U''

négyszög téglalap, ezért

\begin{matrix} \frac{U' U}{U' A} = \frac{C U''}{U' A} = \frac{C P}{A Q} = \frac{C B}{A C}, \end{matrix}

amit bizonyítani akartunk.
Ha

s \equiv C A

, akkor

P \equiv C

és

Q \equiv A

, tehát

P Q \equiv C A

, e helyzetben

U \equiv A \equiv Q

, a

P Q U

háromszög nem létezik, tehát az

A

pont csak tágabb értelemben tartozhat a mértani helyhez. Hasonlóan

s \equiv C B

esetén sincs háromszög, mert

P Q \equiv B C

és

U \equiv C

. Végül akkor sem jön létre a

P Q U ▵

, ha

s

átmegy

p

és

q

második közös pontján ‐ ami nyilván

C

-nek

A B

-re való

C_{1}

vetülete ‐, mert ekkor

P \equiv Q

.
Fordítva megmutatjuk, hogy ha

U

A B

szakasznak

C_{1}

-től különböző tetszés szerinti belső pontja, akkor van

s

-nek olyan helyzete, amely éppen ezen

U

-hoz vezet, éspedig 2 ilyen helyzet is van és ezek

C A

-ra (egyszersmind

C B

-re is) tükrösek. Legyen

p

q

-nak a

90^{\circ}

-os

A C B

szögtartományba ‐ röviden:

γ

-ba ‐ eső félköre

p_{1}

q_{1}

, és a másik félköre

p_{2}

q_{2}

. Messe az

U

-n átmenő,

C A

-val párhuzamos egyenes

p_{1}

-et,

C B

-t,

p_{2}

-t rendre

P

U''

P_{2}

-ben. A mértani helynek az

s

egyenes

C P

és

C P_{2}

helyzetéhez tartozó pontja rajta van

P U''

-n és a már bizonyítottak szerint az

A B

egyenesen, tehát éppen a kiindulásul választott

U

pont.
Mivel

P

és

P_{2}

B C

tengelyre tükrös pontpár, azért

P_{2} C

P C

tükörképe a

B C

tengelyre s ekkor egyben a

B C

-re merőleges

A C

tengelyre is.

U \equiv A

esetén

P \equiv P_{2} \equiv C

;

Q \equiv A

P Q \equiv C A

; ugyanígy

U \equiv B

esetén

P Q \equiv B C

, e helyzetekhez nem tartozik

P Q U

háromszög. Bizonyításunknak a

P_{2}

-re vonatkozó része azonban

U \equiv C_{1}

-re is érvényes.
Ezek szerint az

U

pontok mértani helye valóban az

A B

átfogószakasz, kétszer számítva, de a végpontok nélkül, és

C_{1}

-et csak egyszer számítva.
Egész hasonlóan járhatunk el a

V

pontok mértani helyének meghatározására is. Jelöljük

V

-nek

C A

C B

-re való vetületét

V'

V''

-vel. Ekkor a fenti hasonlóságok felhasználásával

\begin{matrix} \frac{V' C}{V' V} = \frac{P U''}{U' Q} = \frac{P C}{Q A} = \frac{C B}{C A}, \end{matrix}

tehát a

V C V'

és

A B C

derékszögű háromszögek hasonlók, és így

V C V' ∢ = A B C ∢ = C_{1} C A ∢

.
Ha már most

P

p_{1}

félkörön van, és így

Q

q_{1}

-nek pontja, akkor

V

γ

-ban fekszik,

V'

C A

-n van, tehát a nyert egyenlőségből

V C A ∢ = C_{1} C A ∢

, vagyis

V C

azonos a

C_{1} C

egyenessel,

V

C_{1} C

-n fekszik. Ha

P

p_{2}

félkörön, és ezért

Q

q_{2}

-n van, akkor

V

γ

csúcsszögtartományában van,

V'

C A

-nak

C

-n túli meghosszabbításán, tehát egyenlőségünk szerint

V C V'

és

C_{1} C A

csúcsszögek, ezért

V

ekkor is a

C_{1} C

egyenesen van.

C_{1} C

merőleges

A B

-re.
Legyen

p

-nek

C A

-val,

q

-nak

C B

-vel párhuzamos átmérője

D E

, ill.

F G

E

p_{1}

-en,

G

q_{1}

-en. Ekkor

P

-nek és vele

V

-nek

C B

-től legnagyobb távolsága mindkét oldalon

D E / 2 = B C / 2

. Ha

P \equiv E

, akkor

P C B ∢ = 45^{\circ} = P C A ∢

, ezért

C P

q_{1}

-et

Q \equiv G

-ben metszi, amely

q

-nak

C A

-tól ugyancsak legtávolabbi pontja; az ezekhez tartozó

V

-helyzet legyen

V_{1}

. Ha pedig

P

D

-ben van, akkor

Q

F

-be jut, az ezekhez tartozó

V_{2}

a másik oldalon van a lehető legtávolabbra

C B

, ill.

C A

-tól. Ezekkel a fentiekhez hasonlóan megmutatható, hogy a

V

pontok mértani helye a

V_{1} V_{2}

szakasz, kétszer számítva, de kihagyva

C

-t, és csak egyszer számítva a

C_{1}

V_{1}

V_{2}

pontokat. Könnyű belátni, hogy

V_{1} V_{2} = A B

és

C

felezi

V_{1} V_{2}

-t. Ha az

A B C

háromszög egyenlő szárú, akkor

C_{1} \equiv E \equiv G

, és ez a pont nem szerepelhet

V

gyanánt.
Mindezek szerint valamennyi vizsgált derékszögű háromszög harmadik csúcsának mértani helye ‐ míg

s

minden lehetséges helyzetét felveszi ‐ tágabb értelemben az

A B

átfogó és az a rá merőleges, vele egyenlő hosszú

V_{1} V_{2}

szakasz, melynek felezőpontja

C

, mindkettő kétszer számítva. Szigorúan véve ‐ ha ti. az egyenesszakasszá, ponttá fajuló háromszögeket nem tekintjük ‐

A

B

C

nem tartoznak a mértani helyhez,

V_{1}

és

V_{2}

csak egyszer számítandók, a két szakasz

C_{1}

metszéspontja általában összesen kétszer, kivéve a

C A = C B

esetet, amikor

C_{1} \equiv V_{1}

, és ezért csak egyszer számítható.

Megjegyzések. 1. A verseny rövid ideje alatt természetesen nem volt várható, hogy a versenyzők a fenti finomabb diszkussziót is kidolgozzák. Mulasztás lenne viszont, ha itt erre nem tértünk volna ki.
2. Azt, hogy

U

A B

-n,

V

V_{1} V_{2}

-n van, ugyancsak szögek egyenlősége alapján, de hasonló háromszögek felhasználása nélkül is beláthatjuk. Ezt csak

U

esetére és olyan helyzetre vázoljuk, amelyben

P

p_{1}

-beli

C C_{1}

íven van, és így

Q

q_{1}

-beli

A C_{1}

ív pontja.

A Q C_{1} C

és

B C_{1} P C

húrnégyszögek, ezért

P C_{1} Q ∢ = P C_{1} A ∢ + A C_{1} Q ∢ = P C B ∢ + A C Q ∢ = A C B ∢ = 90^{\circ}

. Másrészt szerkesztésnél fogva

P U Q ∢ = 90^{\circ}

, így

P U Q C_{1}

húrnégyszög. Ennélfogva

U C_{1} Q ∢ = U P Q ∢

, és ez folytatólag egyenlő

A C Q ∢

-gel ‐ mert

P U ∥ C A

‐, végül

A C_{1} Q ∢

-gel. Eszerint

C_{1} Q

-val

C_{1} U

és

C_{1} A

egyenlő szöget zár be, tehát

U

C_{1} A

egyenesen van. ‐ Húrnégyszögek felhasználásával igazolható fordítva az is, hogy

A B

és

V_{1} V_{2}

bármely pontja hozzátartozik a mértani helyhez. Ezt és a további helyzetek vizsgálatát az olvasóra bízzuk.