Kezdőlap


Feladat:	1961. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1961/november, 100. oldal		PDF \| MathML
Témakör(ök):	Pitagorasz-tétel alkalmazásai, Arany Dániel
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1961. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $P$ , ill. $Q$ vetülete az $A D$ átmérőn $P'$ , ill. $Q'$ , és jelöljük a háromszög köré irt kör sugarát $r$ -rel. Így a $D$ középpontú $B C$ körív sugara szintén $r$ , a háromszög oldalának és az $A$ középpontú $B C$ körív sugarának hossza pedig $A B = r \sqrt[]{3}$ . $P$ és $Q$ -nak $B C$ -től mért (egyenlő) távolságát jelöljük $d$ -vel, míg $A D$ -től mért távolságuk legyen 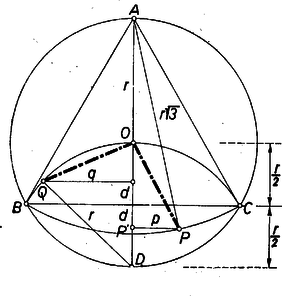$P P' = p$ és $Q Q' = q$ .

Kifejezzük

O P

és

O Q

hosszát

r

-rel és

d

-vel és az így nyert kifejezéseket összehasonlítjuk. Az

O P P'

és az

A P P'

derékszögű háromszögből

\begin{matrix} O P^{2} = {(\frac{r}{2} + d)}^{2} + p^{2}, p^{2} = {(r \sqrt[]{3})}^{2} - {(\frac{3 r}{2} + d)}^{2}, \end{matrix}

és így

\begin{matrix} O P^{2} = 3 r^{2} + {(\frac{r}{2} + d)}^{2} - {(\frac{3 r}{2} + d)}^{2} = 3 r^{2} - r (2 r + 2 d) = r (r - 2 d) . \end{matrix}

Hasonlóan az

O Q Q'

és a

D Q Q'

derékszögű háromszögből

\begin{matrix} O Q^{2} = {(\frac{r}{2} - d)}^{2} + q^{2}, \\ q^{2} = r^{2} - {(\frac{r}{2} + d)}^{2}, \end{matrix}

és így

\begin{matrix} O Q^{2} = r (r - 2 d) = O P^{2} . \end{matrix}

Miután

O P

és

O Q

értelemszerűen pozitívok, eredményünk a feladat állítását bizonyítja.

Megjegyzés. Ha

P

és

Q

mindegyikét a felhasznált köröknek a félkörnél nagyobb ívén vesszük fel a

B C

egyenestől egyenlő távolságban, akkor hasonló számítással ismét azt nyerjük, hogy

P

és

Q

egyenlő távolságra van

O

-tól is.