Feladat: 1960. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 1. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1960/október, 53 - 54. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Középpontos tükrözés, Párhuzamos szelők tételének megfordítása, Arany Dániel
Hivatkozás(ok):Feladatok: 1960/október: 1960. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Gondoljuk a feladatot megoldottnak és legyen a keresett, AB-vel párhuzamos egyenesnek BC-vel, ill. AC-vel alkotott metszéspontja P, ill. Q. A PQ szakasz a kis háromszög és a trapéz kerületének egyaránt része, ezért a kerületek egyenlőségére vonatkozó követelmény így is írható:

PC+CQ=PB+BA+AQ,(1)
és így PC+CQ egyenlő az ABC háromszög kerületének felével.
 
 

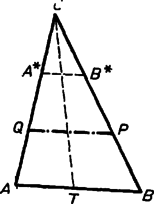Másrészt mivel QP párhuzamos AB-vel, azért a CPQ és CBA háromszögek hasonlók, és így
PC:CQ=BC:CA.(2)

Ezek alapján először k/2=(AB+BC+CA)/2 hosszúságú egyenesszakaszt szerkesztünk, majd ezt BC:CA arányban kettéosztjuk, és így nyerjük a keresett PC, ill. CQ szakaszt.
 
Szerkesztésünk helyessége nyilvánvaló; P mindig a BC szakaszon adódik, mert PC+CQ=k/2 a háromszög-egyenlőtlenség folytán kisebb BC+CA-nál.
 
II. megoldás: Tükrözzük A-t a Q, B-t a P pontra nézve, így nyerjük az A*, B* pontokat. (l)-ből az így létrejött további egyenlő darabokat elhagyva
B*C+CA*=BA.
Másrészt nyilvánvaló, hogy A*B* párhuzamos AB-vel, amiből következik, hogy
B*C:CA*=BC:CA.
Eszerint az AB oldalt a BC és CA oldalak arányában osztva nyerjük a B*C és CA* szakaszokat, a keresett P, Q pont pedig a BB*, AA* szakasz felezőpontja.
 
Megjegyzések: 1. Itt az I. megoldáshoz képest azt nyertük, hogy a felosztandó szakaszt nem kell szerkesztenünk. A felosztás igen egyszerűen adódik az ACB szög CT felezőjével.
2. A feladat általánosítható: előírhatjuk, hogy a kis háromszög és a trapéz kerületei egyenlőség helyett adott λ (λ≠1,λ>0) arányban álljanak:
PC+CQ+QP=λ(PB+BA+AQ+QP),(3)
(ahol λ-t úgy tekintjük adottnak, hogy ismerjük az egységnyi hosszúságú és a λ hosszúságú szakaszt). Előírhatjuk azt is, hogy az (1) két oldalán álló összegek aránya legyen egy adott μ érték:
PC+CQ=μ(PB+BA+AQ).(4)
Ezekkel a feladat így hangzik: Adott az ABC háromszög. Szerkesszük meg a BC oldalon a P, és az AC oldalon a Q pontot úgy, hogy PQ párhuzamos legyen BA-val és teljesüljön (3), ill. (4).
Tekintsük előbb a (4) követelmény esetét. Adjunk (4) mindkét oldalához μ(PC+CQ)-t, így
(1+μ)(PC+CQ)=μ(BC+BA+AC),
másképpen
(PC+CQ):(BC+BA+AC)=μ:(1+μ).(4')
Ennek alapján első lépésül a háromszög kerületéhez és a μ, 1+μ szakaszhoz negyedik arányosként megszerkesztjük PC+CQ-t, majd ezt (2)-nek megfelelően két részre osztjuk.
Megoldás létezésének feltétele, hogy PC+CQ kisebbnek adódjék BC+CA-nál. Ezt (4') csekély átalakításával úgy is mondhatjuk, hogy a μ:1 arány értéke kisebb legyen (BC+CA):AB-nél; egyenlőség esetén a P pont B-be, Q pedig A-ba esik, a trapéz elfajul egyenesszakasszá.
A (3) követelmény esetében a PC=a', QC=b', QP=c', BC=a, AC=b, AB=c egyszerűbb jelölésekkel a fentemlített hasonlóság alapján b'=ba'/a és c'=ca'/a. Ezek alapján (3) így alakítható:
a':a=k:(1+λλk-2c),
amiből a' az előbbi esethez hasonlóan megszerkeszthető.
A megoldhatóság feltétele, hogy a' kisebbnek adódjék a-nál, másképpen, hogy ‐ a legutóbbi aránypárból ‐ a λ:1 arány értéke kisebb legyen k:2c-nél. Egybetűs jelölésekkel a (4) követelmény hasonlóan így alakítható:
a':a=k:1+μμ(k-c).