|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A háromszöget meg tudjuk szerkeszteni, mert ismerjük mind a három oldalát (1. ábra). A és pontok kitűzéséhez ismerjük a háromszög és oldalát, és további adatot ad az a felismerés, hogy az és átlók metszéspontja mindkét átlónak felezőpontja. Így a háromszögből kiadódó szakasz -nek is súlyvonala.
 1. ábra
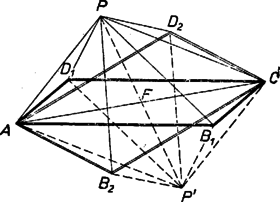
Adatainkból a háromszög megszerkesztése, mint ismeretes, azon alapszik, hogy a háromszöget -re tükrözve és egymás tükörképei lesznek, és tükörképét -vel jelölve a négyszög paralelogramma. Eszerint és , ennélfogva -t a körül és körül sugárral írt körök metszéspontja adja, pedig a paralelogramma negyedik csúcsa lesz.
A kapott négyszög megfelel a követelményeknek, mert csúcsai az előírt távolságokra vannak -től, egyik átlója a kívánt hosszúság, végül a négyszög paralelogramma, mert átlói (-ben) felezik egymást.
Mivel az ábrán -re és , valamint és tükrös párok, azért a háromszöget paralelogrammává egészíti ki. Így -t ismerete nélkül is kitűzhetjük. És mivel -et tovább sem használjuk fel, megszerkesztése mellőzhető. Ezért -et a diszkusszióban nem említjük.
A háromszög és vele az paralelogramma egyértelműen megszerkeszthető, ha az adott , és szakaszok közül bármelyik kettőnek összege nagyobb a harmadiknál. A paralelogramma megszerkeszthető, ha a létrejött és adott , szakaszok közül bármelyik kettő összege nagyobb, mint a harmadik, éspedig 2 megoldást kapunk, ha , ha pedig , akkor egyet. Eszerint -re is a megoldások száma 2. Mert bár a -re adódó két megoldás egybevágó ‐ egymásnak -re tükörképei ‐ a velük adódó paralelogrammák mégsem egybevágók, mert az paralelogrammának általában nem tengelye. Ha azonban , és így rombusz, akkor a ( mellett) adódó két paralelogramma egymásnak -re tükörképe.
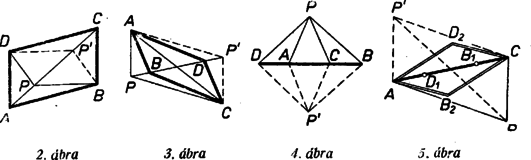
Eljárásunk akkor is használható, ha vagy az első három, vagy pedig az utóbbi három egyenlőtlenség közül az egyikben egyenlőség teljesül, mert ilyenkor és az egyenesre, ill. és a egyenesre esnek, de a 4 pont egy egyenesre esése csak egyszer fordul elő (2-3. ábra). Ha mindkét egyenlőtlenséghármas közül egyben-egyben egyenlőség lép fel, akkor mind a hat pont egy egyenesre esik, a paralelogramma elfajul egyenesszakasszá.
Kivétel a legutóbbi megjegyzésünk alól a eset, amikor az pont -re vonatkozó tükörképének adódik, és így egybeesik -vel, . Ilyenkor ugyanis a paralelogramma is elfajult és vagy egyáltalán nem szerkeszthető még elfajultan sem, ‐ ha ti. ‐ vagy végtelen sokféleképpen szerkeszthető ‐ ha . Ilyenkor tulajdonképpen a két átlójából kellene megszerkeszteni a paralelogrammát.
Megjegyezzük még, hogy az paralelogramma akkor is adódhat elfajultnak, ha sem az , sem a paralelogramma nem elfajult, pl. ha és (4. ábra); sőt az egyik megoldás és esetén is lehet elfajult (5. ábra).
Megjegyzés: A feladat könnyen visszavezethető egy jól ismert négyszögszerkesztési feladatra. Toljuk el a háromszöget úgy, hogy a oldal a vele párhuzamos és egyenlő oldalra kerüljön. Az így keletkező négyszögben adottak az oldalak. Hogy a paralelogramma átlóját is kapcsolatba hozzuk ezzel a négyszöggel, figyeljük meg, hogy a négyszög paralelogramma, s így és átlóinak metszéspontja mindkét átlót felezi. Így az négyszög két nem szomszédos oldalának, -nek és -nek a felezőpontjait összekötő szakasz egyben az háromszögnek középvonala, tehát felével egyenlő, s így adottnak tekinthető. A versenyfeladat tehát ekvivalens a következő ismert feladattal: szerkesszünk négyszöget, ha adott az oldalak hossza és két nem szomszédos oldal felezőpontjának távolsága. A keletkező négyszög adódhat konkávnak vagy hurkoltnak is. (Ezért is kerültük el a ,,szemközti oldalak'' megjelölést.)
Lásd pl. az I. o. gimn. tankönyvben (1959. évi kiadás) a 242. o. 18. feladatában. |
 PDF |
PDF |  MathML
MathML