Kezdőlap


Feladat:	1959. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1959/december, 164 - 166. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Egyenlő szárú háromszögek geometriája, Magasságpont, Háromszögek hasonlósága, Középvonal, Thalesz-kör, Arany Dániel
Hivatkozás(ok):	Feladatok: 1959/szeptember: 1959. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A keresett $A B C$ háromszög ( $A B = A C$ ) alakját megszerkeszthetjük annak alapján, hogy a körülírt kör középpontja a feltételnek megfelelő háromszögekben a szimmetriatengely alap felőli negyedelő pontjával esik egybe. Ez így látható be: legyen az alap felezőpontja $A_{1}$ , a $B$ -ből húzott magasság (amely átmegy az $A A_{1}$ szakasz $M$ felezőpontján) messe $A C$ -t $D$ -ben, az $A_{1}$ -ből $A C$ -re bocsátott merőleges talppontja legyen $E$ . Mivel $M D$ az $A A_{1} E$ háromszögnek, $A_{1} E$ pedig a $B C D$ háromszögnek középvonala, ezért $A D = D E = E C$ . Az $A C$ oldal $F$ felezőpontja tehát $D E$ -t is felezi, így az $F$ -ben $A C$ -re emelt merőleges, ‐ amelynek $A A_{1}$ -gyel való metszéspontja a háromszög köré írt kör $O$ középpontja ‐ az $A_{1} E D M$ derékszögű trapéz középvonala, s így felezi az $A_{1} M$ szakaszt. Ezzel állításunkat igazoltuk.
Ennek alapján a keresett háromszöghöz hasonlót úgy szerkeszthetünk, hogy tetszőlegesen felvesszük az $A A_{1}$ magasságot, ezen megszerkesztjük az $M$ felező- és az $O$ negyedelő pontot. Az $O$ körül $O A$ sugárral írt kör metszi ki az $A_{1}$ pontban $A A_{1}$ -re állított merőlegesből a háromszög $B$ és $C$ csúcsát.
Az $A B C$ háromszögnek a kívánt méretre nagyítását pl. úgy végezhetjük, hogy az adott sugárral megrajzoljuk a ,,hozzáírt'' kört, majd ehhez az $A B C$ háromszög oldalaival párhuzamos érintőket úgy szerkesztünk, hogy a kör a keletkezett háromszög alapját és szárainak meghosszabbítását érintse.

Megjegyzés. Ehhez a szerkesztéshez jutunk az Euler-egyenes tulajdonságainak felhasználásával is, de lényegében erre vezet az is, ha felhasználjuk, hogy a magassági pontot az oldalakra tükrözve a tükörkép a körülírt körre esik. Ismeretes ugyanis, hogy a háromszög

M

magassági pontja,

S

súlypontja ‐ amely mindhárom súlyvonalnak az oldal felőli harmadolópontja ‐ és körülírt körének

O

középpontja ebben a sorrendben egy egyenesen, a háromszög Euler-egyenesén van, ami egyenlő szárú háromszögnél egybeesik a szimmetriatengellyel, és

M S = 2 S O

. ‐ Második észrevételünk alapján pedig az

A A_{1}

szakasz

M

felezőpontjának

A_{1}

-re való

\bar{M}

tükörképét véve

\bar{A M}

-ben a körülírt kör egy átmérőjét nyertük.

II. megoldás: Gondoljuk a feladatot megoldottnak, és messe az

M

-en átmenő,

A C

-vel párhozamos egyenes

B C

-t

G

-ben. Ekkor

M G

A A_{1} C

háromszögnek középvonala, így

C G = G A_{1}

, másrészt

M G

merőleges

M B

-re. ‐ Ennek alapján a tetszőlegesen felvett

B C

alapon megszerkesztjük az

A_{1}

felező és

G

negyedelő pontot,

B G

mint átmérő fölé (Thalész-) félkört írunk, ebből az

A_{1}

-ben

B C

-re emelt merőlegessel kimetsszük

M

-et, végül

A_{1}

-et

M

-re tükrözve kapjuk a keresetthez hasonló

A B C

háromszög hátralevő

A

csúcsát.

III. megoldás: Legyen egy tetszés szerinti

A B C

egyenlő szárú háromszögben (

A B = A C

) a

B C

alap felezőpontja

A_{1}

és az

A A_{1}

szakasz felezőpontja

M

. Meg fogjuk mutatni, hogy a

B M

egyenes és az

A C

oldal

D

metszéspontjából

A A_{1}

-re bocsátott merőleges

T

talppontja az

A A_{1}

szakasz

A

felőli harmadoló pontja, függetlenül a háromszög alakjától. ‐ Ezt tudva a keresett háromszög alakja megszerkeszthető. Egy

a

egyenes egy

A_{1}

pontjában

A A_{1}

merőlegest szerkesztünk, és megszerkesztjük

A A_{1}

-nek az

A

felőli

T

harmadoló pontját. Ekkor az összes olyan

A B C

egyenlő szárú háromszögekben, amelyeknek alapja az a egyenesen van, az alap végpontjait

A A_{1}

felező pontjával összekötő egyeneseknek a szemközti oldallal való metszéspontja a

T

-ben

A A_{1}

-re merőlegesen húzott

t

egyenesen van.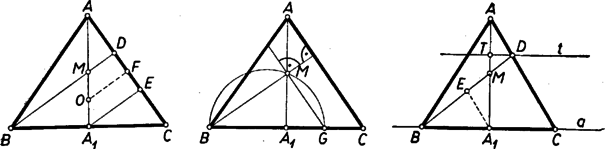

Ennek kell azt a

D_{0}

pontját kikeresnünk, amelyre

A D_{0}

és

B D_{0}

vagy azt, amelyre

A D_{0}

és

C D_{0}

merőlegesek, az ilyen pontokat pedig az

A M

szakasz mint átmérő fölé rajzolt (Thalész-) kör metszi ki

t

-ből. Legyen a kör és az egyenes két metszéspontja

D_{0}

és

D_{0}^{*}

; ezek

A A_{1}

-re szimmetrikusan helyezkednek el, így mindkettőt összekötve

A

-val és az összekötő egyeneseket meghosszabbítva, amíg

a

-t metszik (mondjuk

B

-ben, ill.

C

-ben) egyenlő szárú háromszöget kapunk. Ebben a

B

-t

M

-mel összekötő egyenes

A C

-t annak

t

-vel való metszéspontjában, vagyis

D_{0}^{*}

-ban metszi. Ez rajta van a Thalész-körön is, tehát

B D_{0}^{*}

A C

oldalra bocsátott magasság. Így valóban megszerkesztettük a keresett háromszög alakját ‐ amennyiben a

T

pontra vonatkozó állításunk igaz.
Ennek igazolására húzzunk

A_{1}

-ből párhuzamost

A C

-vel, messe ez

B D

-t

E

-ben.

A_{1} E

B C D

háromszög középvonala, s így

E

felezi a

B D

szakaszt. Másrészt

E M

és

M D

egyenlő, mert

A M D

és

A_{1} M E

háromszögek megfelelő oldalai, ezek pedig egybevágók, ugyanis

A M

és

A_{1} M

oldaluk egyenlő,

M

-nél levő szögeik csúcsszögek,

A

-nál és

A_{1}

-nél levő szögeik pedig váltószögek. ‐ Ekkor azonban

M D

B M

szakasz harmadrésze, s így az

A_{1} B M

és

T D M

hasonló derékszögű háromszögekből (az

M

-nél levő szögek csúcsszögek) nyerjük, hogy

T M

is harmadrésze

A_{1} M

-nek, tehát hatoda

A A_{1}

-nek. Így

A_{1} T

kétharmada és

A T

harmadrésze

A A_{1}

-nek, amint állítottuk.

IV. megoldás. Számítás alapján egy olyan szerkesztést is megadhatunk, amelyben nem szükséges egy hasonló háromszög közbeiktatása.
Jelöljük a háromszög alapját és magasságát

a

-val, ill.

m

-mel, az

a

-val szemközti szögét

α

-val. Legyen az alapot és a szárak meghosszabbítását érintő körnek középpontja

K

(az

A A_{1}

magasság, egyben szögfelező meghosszabbításán), az

A B

egyenesen levő érintési pontja

H

és sugara az adott

ϱ

. Messe a

K H

egyenes a

B C

egyenest az

L

pontban és legyen

A_{1} L = x

. Ezt az

x

hosszúságot fogjuk kiszámítani, majd megszerkeszteni.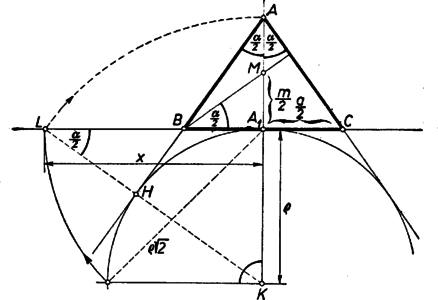

Merőleges szárú hegyes szögekként

B A A_{1} ∢ = K L A_{1} ∢ = α / 2

és

C A A_{1} ∢ = M B A_{1} ∢ = α / 2

, ezért a

K L A_{1}

és

B A A_{1}

, valamint

C A A_{1}

és

M B A_{1}

derékszögű háromszögek hasonlók. A második és az első, ill. a negyedik és az első háromszögből a befogókra:

\begin{matrix} \frac{a}{2} : m = ϱ : x, ill. \frac{m}{2} : \frac{a}{2} = ϱ : x . \end{matrix}

E két aránypárból (egyenletből)

m

-et kiküszöbölve

a

is kiesik (ez úgy is végrehajtható, hogy a két aránypárt tagról tagra összeszorozzuk és egyszerűsítünk), így

x

és

ϱ

között kapunk összefüggést:

\begin{matrix} x^{2} = 2 ϱ^{2}, \end{matrix}

és innen

x = ϱ \sqrt[]{2}

.
Ennek alapján szerkesztésünk a következő: a

ϱ

sugarú körhöz tetszés szerinti

A_{1}

pontjában érintőt szerkesztünk, erre

A_{1}

-től mindkét irányban felmérjük

ϱ \sqrt[]{2}

-t vagyis a

ϱ

befogójú egyenlő szárú derékszögű háromszög átfogóját. A végpontokat a kör

K

középpontjával összekötő egyenesek kimetszik a körből a szárak meghosszabbításainak érintési pontjait.
Megjegyzések. 1.

A

-t a

K A_{1}

félegyenesből

K A = K L

alapján is kimetszhetjük (a

K L A_{1}

és

K A H

derékszögű háromszögek egybevágók).
2. Több versenyző lényegében a legutóbbi gondolatmenettel

α / 2

-t határozta meg: helyesen erre jutott:

{tg}^{2} α / 2 = 1 / 2

, ebből négyzetgyökvonással és trigonometriai táblázattal meghatározta a szöget, és azt szögmérővel felmérte. ‐ Ez az eljárás azonban nem tekinthető (euklidészi) szerkesztésnek.
3. A keresetthez hasonló egyenlő szárú háromszög akkor is megszerkeszthető, ha ‐ a feladattól eltérően ‐ az

M

magasságpontnak felezés helyett valamely más, előírt arányban kell osztania az

A A_{1}

szakaszt. Megoldásaink megfelelő módosítással az

A_{1} M : M A = 1 : k

előírás esetén is használhatók, kivéve az I. megoldást, amelyben lényegesen kihasználtuk, hogy

k = 1

(a hozzáfűzött megjegyzések azonban használhatók). A feladatnak

k

minden (pozitív) értéke mellett egy és csakis egy megoldása van, és ez áll akkor is minden

k < 1

-re, ha

M

-et

A A_{1}

meghosszabbításán kell kapnunk.