Kezdőlap


Feladat:	1959. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1959/november, 85 - 87. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Beírt kör, Hozzáírt körök, Középponti és kerületi szögek, Egyenlő szárú háromszögek geometriája, Arany Dániel
Hivatkozás(ok):	Feladatok: 1959/szeptember: 1959. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Gondoljuk a feladatot megoldottnak, legyen a keresett háromszög $A B C$ , ebben $B C = a$ , $B A C ∢ = α$ és ‐ $O$ -val a beírt $k$ kör középpontját jelölve $A O = d$ az adott szakasz.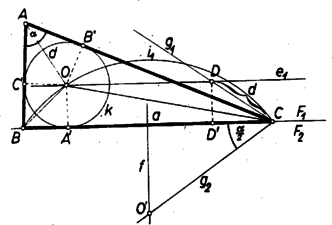

Legyenek továbbá

k

-nak az oldalakon levő érintési pontjai

A'

B'

C'

és sugara

ϱ

. Az

O B C

háromszögben

\begin{matrix} C O B ∢ = 180^{\circ} - O B C ∢ - O C B ∢ = 180^{\circ} - \frac{β}{2} - \frac{γ}{2} = 90^{\circ} + \frac{180^{\circ} - β - γ}{2} = 90^{\circ} + \frac{α}{2} . \end{matrix}

Eszerint

O

csak azon az

i_{1}

i_{2}

körívpáron lehet, amelynek (

B

és

C

-től különböző) pontjaiból az adott

B C

szakasz a megszerkeszthető

90^{\circ} + \frac{α}{2}

szögben látható. Másrészt megszerkeszthetjük

O B' = ϱ

-t, mert az

A O B'

derékszögű háromszög alakját a

d

átfogó és az

α / 2

hegyesszög meghatározza, ‐ és evvel még egy mértani helyet kapunk

O

-ra, ugyanis

O

csak a

B C

-től

ϱ

távolságban fekvő

e_{1}

e_{2}

párhuzamos egyeneseken lehet.
Ezek alapján a szerkesztés a következő. Felvesszük a

B C = a

szakaszt és kijelöljük, hogy a háromszöget a

B C

egyenessel létrejött

F_{1}

és

F_{2}

félsíkok közül

F_{1}

-en kívánjuk kapni.

F_{1}

-en fekszik

O

is, elég lesz tehát az

i_{1}

-et és

e_{1}

-et megszerkesztenünk.

C B

-re a

C

csúcsban mindkét félsíkon felmásoljuk az

α / 2

szöget, a szárak

g_{1}

g_{2}

, megszerkesztjük

B C

-nek

f

felező merőlegesét, majd

g_{2}

és

f

-nek

O'

metszéspontja körül

O' B = O' C

sugárral megrajzoljuk

i_{1}

-et.

e_{1}

-et pedig úgy kapjuk, hogy

g_{1}

-re

C

-ből felmérjük

d

-t, és ennek

D

végpontján át

B C

-vel párhuzamost húzunk.

i_{1}

és

e_{1}

közös pontja

O

, ennek vetülete

B C

-re

A'

és

O A' = ϱ

, ezek alapján megrajzoljuk a

k

kört. Most már az

A

csúcsot a

B

és

C

-ből

k

-hoz húzott második érintők metszéspontja adja. (Ezek céljára

C'

B'

-t a

B

körül

B A'

, ill.

C

körül

C A'

sugárral írt körrel metszhetjük ki.)
Szerkesztésünk helyes, mert a

B C O'

egyenlő szárú háromszög

O'

-nél levő szöge kétszerese

α / 2

pótszögének, azaz

180^{\circ} - α

, ez egyben a

O'

középpont körül

O' B

sugárral írt kör

F_{1}

-beli

i_{1}

ívéhez tartozó középponti szög. Így a kör

F_{2}

-beli ívéhez

180^{\circ} + α

nagyságú középponti szög tartozik, tehát a

B O C

kerületi szög ennek fele:

90^{\circ} + α / 2

. Most már a

C' B C

és

B' C B

szögek összege kétszerese az

O B C

és

O C B

szögek összegének, a

B O C

szög kiegészítő szögének,

90^{\circ} - α / 2

-nek, azaz

180^{\circ} - α

-val egyenlő, tehát a szerkesztett érintők

A

-nál valóban

α

szöget zárnak be (az a szögük ekkora, amelynek terében a

B C

szakasz van).

A O

felezi az

A

-ból

k

-hoz húzott érintők szögét, ezért

O A B' ∢ = α / 2 = D C B ∢

, továbbá

D

-nek

B C

-n levő vetületét

D'

-vel jelölve az

A O B'

és

C D D'

derékszögű háromszögekben

O B' = O A' = D D'

, így e két háromszög egybevágó, tehát

A O = C D = d

.
A szerkesztés lépései

O

előkészítéséig egyértelműen végrehajthatók (

α

nyilván

0^{\circ}

és

180^{\circ}

közti szög, így fele hegyesszög).

i_{1}

és

e_{1}

közös pontjainak száma szerint

O

-ra

2

1

0

pontot kapunk, és ezekből ugyanennyi háromszöget, mert a további lépések ismét egyértelműek. Ha

2

megoldás adódik, ezek egybevágók, mert egymásnak

f

-re nézve tükrös párjai, így a feladatnak lényegében legfeljebb

1

megoldása van.

II. megoldás: Az adott

α

szög az

a

oldal látószöge az

A

csúcsból, ennek alapján ismert módon megszerkeszthetjük a keresett háromszög

k^{*}

körülírt körét.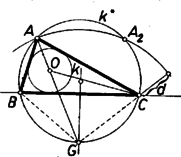

B A C

szög

A O

felezője

k^{*}

-ot másodszor az

A

-t nem tartalmazó

B C

ívnek

G

felezőpontjában metszi, mert a kerületi szögek tétele szerint

G B C ∢ = G A C ∢ = G A B ∢ = G C B ∢ = α / 2

, tehát a

B C G

háromszögben

G B = G C

, és e húrokhoz egyenlő ívek tartoznak. Másrészt

C O

felezi az

A C B

szöget, ezért az

O C G

háromszögben

O C G ∢ = (γ + α) / 2

. Ekkora a

C O G

szög is, mint az

A C O

háromszög külső szöge, tehát a

C O G

háromszög egyenlő szárú:

O G = C G

. Így

A

-nak

G

-től való távolsága

A G = A O + O G = d + C G

.
Ezek alapján a szerkesztés a következő.

k^{*}

-ban a

B C

-re merőleges átmérőnek az a végpontja

G

, ahonnan

B C

látószöge

180^{\circ} - α

. (Ez is mutatja, hogy

G

azonos az I. megoldásban használt

O'

-vel.) A

G C

szakasznak

C

-n túli meghosszabbítására rámérjük

d

-t. A

G

körül

d + C G

sugárral leírt kör

k^{*}

-ból kimetszi

A

-t. Aszerint, hogy a

d + C G

szakasz kisebb, ill. nagyobb

k^{*}

átmérőjénél, ill. éppen egyenlő vele,

2

0

, ill.

1

megoldást kapunk. ‐ Szerkesztésünk helyessége bizonyításául csak azt kell megmutatnunk, hogy a kapott

A

pontot

G

-vel összekötő szakasznak

A

-tól

d

távolságra, azaz

G

-től

C G

távolságra fekvő

O^{*}

pontja azonos az

A B C

háromszögbe írt kör középpontjával. Valóban, a

C G O^{*}

háromszög egyenlő szárú, és benne

C G O^{*} ∢ = C B A ∢ = β

, így

O^{*} C G ∢ = 90^{\circ} - β / 2

, ennélfogva

O^{*} C B ∢ = O^{*} C G ∢ - B C G ∢ = O^{*} C G ∢ - α / 2 = 90^{\circ} - (α + β) / 2 = γ / 2

, vagyis

O^{*} C

felezi a

C

-nél fekvő szöget. Másrészt

O^{*}

A

-nál fekvő szög felezőjén is rajta van, tehát

O^{*} = O

III. megoldás: Az előbbi

A O B'

háromszöggel egybevágó háromszöget szerkesztve megkapjuk

A B'

-t, az

A

-ból

k

-hoz húzható érintőszakaszt. Erről ismeretes, hogy egyenlő

s - a

-val, ahol

s

a háromszög kerületének fele. Ebből (a szokásos jelölésekkel)

b + c = 2 s - a = 2 (s - a) + a

alapján előállíthatjuk az

A

csúcsból kiinduló oldalak összegét, ezzel pedig a feladatot visszavezettük a háromszögnek az

a

b + c

α

adathármasból való ismert szerkesztésére: az

A^{*}

csúcsú

α / 2

szög egyik szárára felmérjük

b + c

-t, ennek

B

végpontjából

a

sugarú körívvel a másik szárból kimetsszük

C

-t, majd

A^{*} C

felező merőlegesével az első szárból

A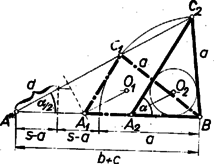

-t.

A körívnek a szög szárával

2

1

0

közös pontja, egyszersmind ennyi megoldás van. Két metszéspont esetén mindkettő

A^{*}

-nak ugyanazon oldalára esik (különben

a > b + c

volna), ezért

A_{1}

és

A_{2}

A^{*} B

szakaszra esnek. Az így adódó

A_{1} B C_{1}

és

A_{2} C_{2} B

háromszögek egybevágók. Ugyanis az

A^{*} C_{1} A_{1}

és

A^{*} C_{2} A_{2}

egyenlő szárú háromszögek külső szögeként

C_{1} A_{1} B ∢ = C_{2} A_{2} B ∢ = α

, másrészt

A^{*} C_{1} A_{1} ∢ = A^{*} C_{2} A_{2} ∢ = α / 2

C_{1} B A_{1} ∢ = ε

jelöléssel

B C_{1} A_{1} ∢ = 180^{\circ} - α - ε

, így

C_{2} C_{1} B ∢ = 180^{\circ} - (180^{\circ} - α - ε) - α / 2 = ε + α / 2

. Ámde a

B C_{1} C_{2}

háromszög egyenlő szárú, ezért

C_{1} C_{2} B ∢ = ε + α / 2

, tehát

A_{2} C_{2} B ∢ = ε

. Így a kérdéses háromszögek egy oldalban és két megfelelő szögben megegyeznek, valóban egybevágók.

IV. megoldás:

α

és

d

ismeretében megszerkeszthető

O

k

és

α

szárainak az érintési pontig terjedő szakasza:

s - a

. Ezzel egyúttal

(s - a) + a = s

is ismert, a csúcstól ekkora távolságban érinti

α

szárait az

a

oldalt kívülről érintő

k_{1}

hozzáírt kör, így ez is megszerkeszthető.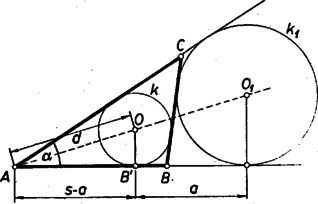

Most már

k

és

k_{1}

közös belső érintőinek az

α

szög szárai közé eső szakasza az

a

oldal.