Feladat: 1959. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1959/október, 46 - 48. oldal  PDF  |  MathML 
Témakör(ök): Pont körüli forgatás, Arany Dániel
Hivatkozás(ok):Feladatok: 1959/október: 1959. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata

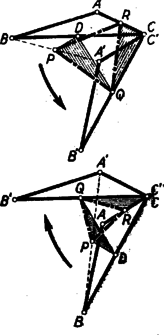
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kérdéses felezőpontokat rendre P, Q, R-rel jelölve azt bizonyítjuk, hogy a PQR háromszögnek QP és QR oldalai egyenlők és egymásból 60∘-os elforgatással állnak elő. Evégett a BC oldal D felezőpontját segítségül véve megmutatjuk, hogy a QDP háromszög 60∘-os forgatással áll elő a QCR háromszögből.

 
 

A QD szakasz a CB'B szabályos háromszögnek középvonala, így a CQD háromszög is szabályos, tehát a Q pont D-ből az eredeti forgatással áll elő, és QD=QC; továbbá QD ugyanazon irányú 60∘-os forgatással keletkezik QC-ből, mint amelyikkel CQ a CD-ből, vagyis amelyik forgatással A'B'C'-t az ABC-ből képeztük. Hasonlóan a DP szakasz a CBA' háromszögnek középvonala, így fele a CA' oldalnak, egyszersmind CA-nak is ‐ mert a CA'A háromszög szabályos ‐, tehát egyenlő CR-rel; továbbá DP-nek és CA'-nek iránya ugyancsak az eredeti forgatással áll elő CA, azaz CR irányából.
Ezek szerint a QDP szög szárai a QCR szög száraiból ugyanakkora és ugyanazon irányú forgatással állnak elő, tehát e két szög egyenlő. Egyenlők a QDP és QCR háromszögeknek e szögek megfelelő szárain fekvő oldalai is, így a két háromszög egybevágó, és egymáshoz képest valóban 60∘-kal vannak elfordulva. Ennélfogva harmadik megfelelő oldalpárjukra QP=QR, és RQP∢=60∘, amit bizonyítani akartunk.
Megjegyzések. 1. Az ábra több más módon is kiegészíthető oly egybevágó háromszögekkel, amelyek segítségével a PQR háromszög két oldalának egyenlősége bizonyítható. A versenyzők általában a fenti bizonyításénál bonyolultabb utakat követtek; alig volt két versenyző, aki egyformán bizonyított volna. Egyesek nem vették észre, hogy könnyű meghatározni a PQR háromszög két oldalának szögét, ehelyett külön bizonyították be további két oldal egyenlőségét.
2. Az előbbi gondolatmenettel bizonyítható tételünknek következő általánosítása. Ha az ABC háromszögnek a C csúcsa körüli 60∘-os elforgatása után az A'B, CB' és AC' szakaszokat tetszőleges, de ugyanazon arány szerint osztjuk (pl: mindegyiket harmadoljuk), az osztópontok szabályos háromszöget alkotnak.
3. Néhány versenyző észrevette bizonyítandó tételünk kapcsolatát a következő tétellel:* ,,Az OAB és OA'B' ellentétes körüljárású szabályos háromszögek O csúcsa közös. Bizonyítsuk be, hogy ... az AA', OB és OB'... szakaszok felezőpontjai szabályos háromszög csúcsai.'' ‐ A versenyfeladatban az ABC háromszög 60∘-os elforgatása során keletkező CAA' és CB'B háromszögek C csúcsa közös, és körüljárásuk ellentétes. Ábránk betűzését úgy átírva, hogy a közös csúcs jele C, ill. C' helyett O legyen, a többi csúcsé pedig A, B, A' és B' helyett rendre B, A', A és B', tüstént látjuk, hogy az idézett állítás éppen a PQR háromszög szabályosságát mondja ki.
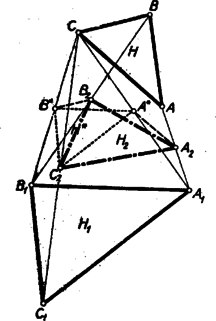
4. A feladatot felfoghatjuk úgy is, hogy az AA'C és C'BB' egyező körüljárású szabályos háromszögek megfelelő csúcsait összekötő szakaszok felezőpontjairól mutattuk meg, hogy újabb szabályos háromszöget alkotnak. Ebben a formában a feladat lényegesen általánosítható, amennyiben sem a közös csúcsnak, sem a háromszögek szabályos voltának nincs benne lényeges szerepe.
Legyen ABC és A1B1C1 két hasonló, egyező körüljárású háromszög, ekkor az AA1, BB1, CC1 szakaszok A2, B2, C2 felezőpontjai is az ABC háromszöghöz hasonló és egyező körüljárású háromszöget alkotnak.
Ez a tétel is könnyen bizonyítható komplex számok segítségével,* de a versenyfeladat fenti bizonyításához hasonlóan is bizonyítható.
Nevezzük az állításban szereplő háromszögeket a csúcsok indexezésének megfelelően H, H1 és H2 háromszögnek. Összekötve C-t az A1 és B1 csúccsal is, a keletkező szakaszok felezőpontja legyen A* és B*. Mivel A*B*C2 ‐ amit a továbbiakban H*-gal fogunk jelölni ‐ H1-nek C-ből felére kicsinyített képe, így elég H2 és H*-ról megmutatni, hogy hasonlók és egyező körüljárásúak.
 
 

A2A* és A*C2 mint az AA1C, ill. A1CC1 háromszög középvonala párhuzamos és egyirányú az AC, ill. A1C1 szakasszal és fele akkora. Hasonlóan B2B* és B*C2 mint a BB1C, ill. B1CC1 háromszög középvonala a BC, ill. B1C1 szakasszal párhuzamos, egyező irányú és fele akkora. Így az A2A*C2 háromszögben az A*-nál levő szög és B2B*C2-ben a B*-nál levő szög egyaránt annak a szögnek a kiegészítő szögével egyenlő, amellyel H1-el van forgatva H-hoz képest, az ezeket a szögeket közrefogó oldalak aránya pedig (mindkétszer a fönti sorrendben véve) H és H1 megfelelő távolságainak arányával egyezik meg. Ebből következik, hogy az A2A*C2 és B2B*C2 háromszögek hasonlóak és egyező körüljárásúak. Ekkor azonban A2C2 az A*C2-ből és B2C2 a B*C2-ből egyező irányú és nagyságú elforgatással és ugyanolyan arányú nyújtással keletkezik, s így ugyanezzel az elforgatással és nyújtással keletkezik H2 is H*-ból. Ezzel állításunkat igazoltuk.
A bizonyítás könnyen láthatóan abban az esetben is érvényben marad, ha egyes szereplő háromszögek egyenesszakasszá fajulnak. Ez bekövetkezik akkor is, ha H és H1 szerepét a versenyfeladat AA'C és C'BB' háromszögének adjuk át. Ekkor A* a C≡C' ponttal esik egybe, B*-nak pedig a feladatmegoldás D pontja felel meg.
* Lásd Reiman István: Geometriai feladatok megoldása a komplex számsíkon, 48. feladat, 63. és 71. o. Tankönyvkiadó 1957, Középiskolai Szakköri Füzetek.

*Lásd ugyanott, 77. o. 9. Példa.