Feladat:	1959. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 2. feladata	Korcsoport: 14-15	Nehézségi fok: könnyű
Füzet:	1959/október, 42 - 43. oldal		PDF  |  MathML
Témakör(ök):	Szabályos sokszögek geometriája, Paralelogrammák, Arany Dániel
Hivatkozás(ok):	Feladatok: 1959/október: 1959. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.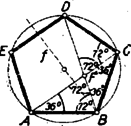   I. megoldás: Legyen az $ABCDE$ szabályos ötszög $AC$ és $BD$ átlóinak metszéspontja $F$. Az $AF=AB$ egyenlőséget abból mutatjuk meg, hogy az $ABF$ háromszögnek $BF$-en fekvő két szöge egyenlő (1. ábra).     1. ábra   Minden (konvex) ötszög szögeinek összege $3\cdot {180}^{\circ }={540}^{\circ }$. A szabályos ötszög szögei egyenlők, így egy-egy szöge ${108}^{\circ }$. Az ötszög köré írható körből az oldalak, mint egyenlő húrok, egyenlő íveket metszenek le. Az ötszög mindegyik szögének szárai között három ilyen ív fekszik, ezért mindegyik ív az ötszög csúcsaiból ${108}^{\circ }:3={36}^{\circ }$-nyi szögben látható. Eszerint $BAF\sphericalangle =BAC\sphericalangle ={36}^{\circ }$, $ABF\sphericalangle =ABD\sphericalangle =2\cdot {36}^{\circ }={72}^{\circ }$, így $AFB\sphericalangle ={180}^{\circ }-\left({36}^{\circ }+{72}^{\circ }\right)={72}^{\circ }=ABF\sphericalangle$, amit bizonyítani akartunk. Az $AF$ szakasz az $AC$ átlónak nagyobbik darabja: $AF>FC$, mert az $ABF$ háromszögben $AF$, az egyik ${72}^{\circ }$-os szöggel szemben fekvő oldal, nagyobb $BF$-nél, a ${36}^{\circ }$-os szöggel szemben fekvő oldalnál, $BF$ pedig egyenlő $FC$-vel, mert a $BCF$ háromszög ‐ két ${36}^{\circ }$-os szöge révén ‐ ugyancsak egyenlő szárú. Hasonlóan látható be, hogy $DF=DC$, és hogy $DF>FB$. ‐ Ezzel a bizonyítást befejeztük. 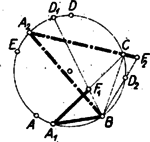  Megjegyzések. 1. A bizonyítás első része csak azt használta fel, hogy a (rövidebb) $BC$ ív egy, és hogy a (rövidebb) $DA$ ív két ötödrésze a kör kerületének. Eszerint az $AF=AB$ egyenlőség érvényes marad akkor is, ha a $DA$ ívet a körön elforgatjuk (2. ábra). ‐ Vegyük észre, hogy az $E$ csúcs a bizonyítás egyik részében sem szerepel.     2. ábra   2. Az $AFB\sphericalangle =ABF\sphericalangle$ egyenlőséget a mértékszámok kiszámítása nélkül is megmutathatjuk. Az $ABD$ szög két ötszögoldalhoz tartozó íven nyugvó kerületi szög, a $CBD$ és $ACB$ kerületi szögek pedig egy-egy ilyen íven nyugszanak. Így az utóbbiak összege egyenlő az $ABD$ szöggel, másrészt ez az összeg a $BCF$ háromszög külső szögeként a $BFA$ szöggel is egyenlő. ‐ Itt viszont csak azt használtuk fel, hogy az $ABCD$ húrnégyszög oldalai által lemetszett körívekre fennáll az $\widehat{AB}+\widehat{CD}=\widehat{AD}$ egyenlőség. Tehát tulajdonképpen a következő általánosabb tételt bizonyítottuk be: ha az $ABCD$ húrnégyszögben fennáll az $\widehat{AB}+\widehat{CD}=\widehat{AD}$ egyenlőség, akkor $AF=AB$ és $DF=DC$, ahol $F$ az $AC$ és $BD$ átlók metszéspontja. (Mindkét átlónak van egy oldallal egyenlő darabja, ahogyan az eredeti tétel is állítja.) Ennek a tételnek egy más bizonyítása: az $A$ körül $AB$ sugárral írt $k_1$ körnek az $ABCD$ négyszög $k$ körülírt körével való második közös pontját $E$-vel jelölve (3. ábra) $\widehat{DE}=\widehat{AD}-\widehat{AE}=\widehat{AD}-\widehat{AB}=\widehat{DC}$, tehát a $D$ körül $DC$ sugárral írt $k_2$ kör szintén $E$-ben metszi 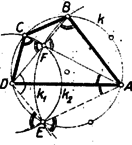$k$-t.     3. ábra   Így $EDA\sphericalangle =BDA\sphericalangle =FDA\sphericalangle$ és $EAD\sphericalangle =CAD\sphericalangle =FAD\sphericalangle$, tehát az $AE$ egyenes az $AF$-nek, $DE$ a $DF$-nek tükörképe $AD$-re, vagyis $E$ az $F$ tükörképe $AD$-re. Eszerint $AF=AE=AB$ és $DF=DE=DC$; egyszersmind $F$ a $k_1$ és $k_2$-nek második közös pontja. (Az $E$ pont megfelel a szabályos ötszög ötödik csúcsának.) ‐ Az állítás hurkolt négyszögre is érvényes, hacsak $B$ és $C$ a $k$ ugyanazon $AD$ ívének pontjai (4. ábra; a 3-4. ábrákon $A$, $B$, $C$, $D$ egy-egy szabályos $7$-, ill. $9$-szög csúcsai közül valók). 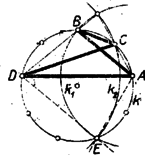    4. ábra   II. megoldás: A kívánt egyenlőséget abból bizonyítjuk, hogy az $AFDE$ négyszög paralelogramma. Az I. megoldás szerint a $CDE$ szög ${108}^{\circ }$, a $DCA$ szög ${72}^{\circ }$, egymásnak kiegészítő szögei. Ámde tudjuk, hogy ha két szög egymást ${180}^{\circ }$-ra egészíti ki, és egyik pár száruk párhuzamos ‐ vagy egybeeső ‐, második száraikba pedig az elsőkből ellentétes irányú forgással jutunk ‐ amint az említett szögek közös $CD$ szárából $DE$-be negatív (az óramutató forgásával egyenlő irányú) forgás visz át, $CA$-ba pedig pozitív ‐, akkor a második szárak ‐ itt $DE$ és $AC$ ‐ szintén párhuzamosak. Ugyanígy a $BD$ átló párhuzamos az $AE$ oldallal. Az így létrejövő $AFDE$ paralelogrammából $AF=ED$ és $DE=AE$, amit bizonyítani akartunk.   Megjegyzés. Számos versenyző szemlélet alapján elfogadta, hogy a szabályos ötszög mindegyik átlója párhuzamos egy oldallal, vagy más szóval, hogy pl. az $ACDE$ négyszög trapéz. Ezt valamivel indokolni kellett volna. Lehet így is: az $ED$ oldal $f$ felező merőlegese szimmetriatengelye az ötszögnek, tehát $A$ és $C$ egymásnak tükörképei $f$-re. Ezért $AC$ merőleges $f$-re, és így párhuzamos $ED$-vel.