Feladat: 1958. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1958/november, 76 - 79. oldal  PDF  |  MathML 
Témakör(ök): Pont körüli forgatás, Transzformációk szorzata, Arany Dániel
Hivatkozás(ok):Feladatok: 1958/október: 1958. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Szerkesszük meg először valamely ABC háromszöghöz az A1B1C1 háromszöget (1. ábra), majd az így nyert ábrát próbáljuk meg úgy kiegészíteni,hogy a szerkesztést visszafelé is elvégezhessük.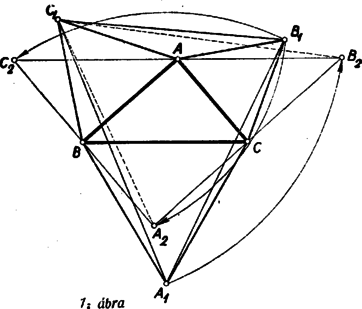

 
 

A szabályos háromszögek mindegyik szöge 60∘-os, ezért célszerűnek látszik 60∘-os elforgatásokat alkalmazni. Forgassuk pl. az ábra C1BA1 háromszögét a C1 pont körül befelé (pozitív értelemben), ekkor a 60∘-os elforgatással a B pont az A pontba kerül, az A1 pont elforgatott helyzetét jelöljük B2-vel. Miután BA1 szakasz 60∘-kal fordult el, párhuzamos helyzetbe került BC-vel, és tekintve, hogy egyenlő is vele, ezért a BCB2A négyszög paralelogramma. Ha most a C1AB1 háromszöget forgatjuk el ugyancsak befelé (ezúttal negatív értelemben) a C1 pont körül, a BACA2 paralelogrammát nyerjük (A2-vel B1 pont elforgatott helyzetét jelöltük). Miután a két paralelogramma közös oldala AB, egy további közös csúcsuk C, így az A2, B2 és C pontok egy egyenesbe esnek és C az A2B2 szakasz felezőpontja. A2 és B2 az adatokból megszerkeszthető, tehát ezekkel együtt C pont is, végül ugyanezzel az eljárással, amivel C-t nyertük, megszerkeszthetjük A-t és B-t. A szerkesztéssel arra jutunk, hogy a keresett ABC háromszög csúcspontjai az A1B1C1 háromszög oldalai fölé befelé rajzolt szabályos háromszögek harmadik csúcspontjai által alkotott A2B2C2 háromszög oldalainak felező pontjai.
A szerkesztés szerint a kitűzött feladat látszólag minden esetben egyértelműen megoldható. Ennek ellentmond a 2. ábrán bemutatott helyzet, amellyel az A1B1C1 háromszögből kiindulva kapunk ugyan ABC háromszöget, de A1, B1 és C1 nem az oldalakra kifelé, hanem a befelé rajzolt szabályos háromszögek harmadik csúcspontja.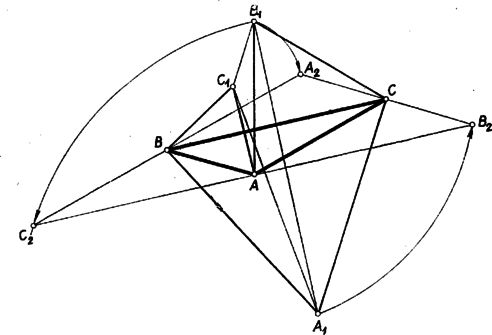
 
 
2. ábra
 

Ezen az ábrán azonban az A1B1C1 háromszög nem hegyesszögű; vegyük észre továbbá azt is, hogy az A2B2C2 háromszög körüljárási értelme ellentétes az A1B1C1 háromszögével.
Bizonyítás nélkül megjegyezzük a következőket. A feladat megoldhatóságának az a feltétele, hogy az A1B1C1 háromszög oldalai fölé befelé rajzolt szabályos háromszögek harmadik csúcsai által alkotott A2B2C2 háromszög körüljárási értelme megegyezzék az A1B1C1 háromszög körüljárási értelmével. (ABC körüljárási értelme mindig megegyezik A2B2C2 körüljárási értelmével.) Az eredeti értelmezés szerint sohasem kapunk megoldást, ha az A1B1C1 háromszögnek van 120∘-osnál nagyobb szöge, és a fennmaradó esetekben mindig kapunk megoldást, ha az A1B1C1 háromszögnek nincs 30∘-osnál kisebb szöge.
 

II. megoldás: A keresett háromszög C csúcsát pl. az jellemzi, hogy alkalmas irányban (C-től A felé) B1 körül 60∘-kal elforgatva, majd C1 körül ugyanilyen irányban 60∘-kal forgatva és végül A1 körül ugyancsak 60∘-kal elforgatva visszakerül eredeti helyzetébe.
Megmutatjuk, hogy ha ugyanezeket a forgatásokat a sík egy tetszés szerinti P pontjára alkalmazzuk, akkor a pont a kiindulási helyzetéből a második forgatás utáni helyzetbe átvihető egy alkalmas pont körüli 120∘-os forgatással, a harmadik forgatás utáni helyzetébe pedig egyetlen alkalmas 180∘-os forgatással, ahol ezek a forgatások egy-egy csak az A1, B1 és C1 pontoktól függő középpont körül történnek.
A bizonyításhoz azt fogjuk felhasználni, hogy egy K pont körül α szöggel történő elforgatás eredményét úgy is megkaphatjuk, ha húzunk a K ponton át tetszés szerint két egyenest, t1-et és t2-t úgy, hogy a t1-től a t2-ig a forgatás irányában α/2 nagyságú szög legyen és minden pontot tükrözünk először t1-re, azután t2-re. Fordítva: két ilyen tükrözés eredménye egy K körüli α nagyságú elforgatással is megkapható (3‐4. ábrák).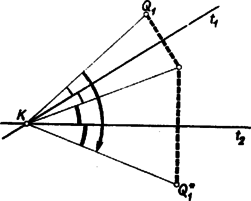
 
 
3. ábra
 
 
4. ábra
 

A B1 körüli forgatást állítsuk elő úgy két tükrözés segítségével, hogy a második tükrözés t2 tengelyéül a B1C1 egyenest választjuk, a C1 körüli forgatást pedig úgy, hogy az első tükrözés t'1 tengelyéül választjuk B1C1-et (5. ábra).
 
 
5. ábra
 

Ekkor egy tetszés szerinti pont a kétszeri forgatás után ugyanoda kerül, mintha tükrözzük a pontot t1-re, a kapott pontot t2(=B1C1)-re, az így nyert pontot t'1(=B1C1)-re, majd az újabb tükörképet t'2-re. A B1C1 egyenesre történő kétszeri tükrözés azonban visszaviszi a pontot az e tükrözések előtti helyzetébe, s így az első két forgatás eredménye ugyanaz, mintha tükrözzük a sík pontjait t1-re, majd t'2-re. Ennek a két tükrözésnek pedig ugyanaz az eredménye, mintha a két egyenes O1 metszéspontja körül végzünk (t1,t'2)=60∘ kétszeresényi, azaz 120∘-os elforgatást. Ezután még A1 körül kell 60∘-kal forgatni.
Ezeket a forgatásokat is állítsuk elő tükrözésekkel úgy, hogy két egymásutánt tükrözés tengelye O1A1 legyen. Ekkor az O1-en átmenő első tükrözési tengelyhez t''1-höz 60∘-kal kell elforgatva lennie O1A1-nek, az A1-en átmenő második tükrözés t2* tengelye pedig 30∘-kal lesz elforgatva O1A1-hez képest. A négy egymásutáni tükrözés ‐ és ezzel együtt a B1, C1, majd A1 körüli 60∘-os elforgatások ‐ végeredménye ekkor ugyanaz, mintha tükrözünk a t''1 egyenesre, azután t2*-ra. E két egyenes metszéspontját O2-vel jelölve A1O1O2 egy 30∘, 60∘, 90∘-os szögekkel rendelkező háromszög, így a három forgatás egymásutáni elvégzésével minden pont ugyanoda kerül, mintha O2 körül forgatnánk el 180∘-kal, azaz tükröznénk az O2 pontra.
Azt a C pontot kerestük, amely a tárgyalt 3 forgatás, vagy ami ugyanarra az eredményre vezet, az O2-re történő tükrözés után eredeti helyére kerül vissza, ilyen pont pedig egyedül O2. A fenti gondolatmenet szerkesztési eljárást is ad C=O2 megszerkesztésére. Az ABC háromszög további csúcsai ugyanezen a módon szerkeszthetők, vagy megszerkeszthetjük C ismeretében a BCA1 és CAB1 egyenlőoldalú háromszögeket.