Kezdőlap


Feladat:	1958. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1958/október, 43 - 45. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Terület, felszín, Arany Dániel
Hivatkozás(ok):	Feladatok: 1958/október: 1958. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A megoldók egy része számítással igazolta az állítás helyességét. Bemutatunk egy ilyen megoldást. Legyen a $P$ pont távolsága az $A B$ és $C D$ oldaltól $m$ , ill. $n$ (1. ábra).

1. ábra

A P C P'

paralelogramma

t

területét megkapjuk, ha az

A B C D

paralelogramma területéből elhagyjuk az

A B C P'

és

A P C D

négyszögek területét.
Az utóbbi két terület egyenlő, mert az idomok egymás tükörképei az

A B C D

paralelogramma középpontjára nézve, így elegendő pl. az

A P C D

négyszög területének kétszeresét vonni le. Ezt a négyszöget az

A P T

és

P C S

háromszögekre, továbbá a

P S D T

paralelogrammára bontva, azt kapjuk, hogy

\begin{matrix} t = A B \cdot (m + n) - A Q \cdot m - Q B \cdot n - 2 A Q \cdot n = (A Q + Q B) (m + n) - \\ - A Q \cdot m - Q B \cdot n - 2 A Q \cdot n = Q B \cdot m - A Q \cdot n . \end{matrix}

Itt a kisebbítendő a

P R B Q

paralelogramma területét, a kivonandó pedig a

P S D T

paralelogrammáét adja. Ezzel igazoltuk a feladat állítását.

Megjegyzés. Az ábrán

P

A C D

háromszögben van. Ez esetben az

A P C D

négyszög konkáv. Ha az

A B C

háromszögben levő

P

pontból indulunk ki, akkor számításunk negatív jellel adja a kiszámítandó paralelogramma területét, annak megfelelően, hogy az említett négyszög ez esetben konvex, és tükörképével együtt kétszeresen fedi az

A P C P'

paralelogrammát.
Számítás nélkül, közvetlenül is belátható a feladatban szereplő területek egyenlősége. A következőkben erre mutatunk két utat.

II. megoldás: Húzzunk

P'

ponton át

A B

-vel és

B C

-vel párhuzamos egyenest, és messék ezek

B C

-t, ill.

A B

-t az

R'

és

Q'

pontban.
Az

A P C P'

paralelogrammát körülzáró két konkáv négyszög egyikét, pl. az

A P' C B

négyszöget vágjuk szét az

A P' Q'

és

P' C R'

háromszögre, valamint a

P' R' B Q'

paralelogrammára (2. ábra).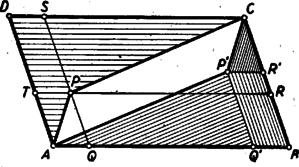

2. ábra

Fedjük le az

A P' Q'

háromszöggel a

P C R

háromszöget. (

A P' Q' ▵ = P C R ▵

, mert

A P' = P C

és a két háromszög szögei egyenlők.) Továbbá a

P' C R'

háromszöggel lefedjük

A P Q

háromszöget, a

P' R' B Q'

paralelogrammával pedig a

P T D S

paralelogrammát (3. ábra).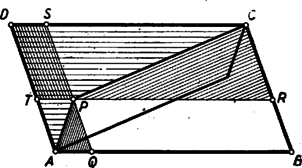

3. ábra

Ezek után az

A B C D

paralelogrammából a két konkáv négyszöggel lefedetlen marad a

P R B Q

paralelogramma, kétszeresen fedett a

P S D T

paralelogramma. Ezért

\begin{matrix} T_{A P C P'} = T_{P R B Q} - T_{P S D T} \end{matrix}

III. megoldás: Messe a

T R

egyenes az

A C

átlót a

P^{\circ}

pontban. Húzzunk

P^{\circ}

ponton át

A D

-vel párhuzamos egyenest, mely

A B

-t

Q^{\circ}

-ban,

C D

-t pedig

S^{\circ}

-ban metszi (4. ábra).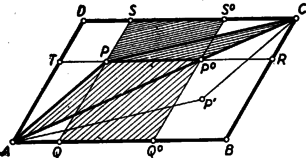

4. ábra

Kimutatjuk, hogy az

A P C P'

paralelogramma területe egyenlő a

Q Q^{\circ} S^{\circ} S

paralelogramma területével, és ugyanezzel egyenlő a

P Q B R

és

P S D T

paralelogrammák területének különbsége is.

P P^{\circ} C △

területe fele a

P P^{\circ} S^{\circ} S

paralelogramma területének, mert

P P^{\circ}

oldaluk és ehhez tartozó magasságuk megegyezik. Hasonló okból

P P^{\circ} A △

területe fele a

P P^{\circ} Q^{\circ} Q

paralelogramma területének. Eszerint az

A P C P'

paralelogramma területe, mely az

A P C △

területének kétszerese, valóban egyenlő a

Q Q^{\circ} S^{\circ} S

paralelogramma területével.
Ismeretes továbbá, hogy

\begin{matrix} T_{P^{\circ} S^{\circ} D T} = T_{P^{\circ} Q^{\circ} B R} . \end{matrix}

\begin{matrix} T_{P^{\circ} S^{\circ} D T} = T_{P S D T} + T_{P^{\circ} S^{\circ} S P}, \end{matrix}

és

\begin{matrix} T_{P^{\circ} Q^{\circ} B R} = T_{P Q B R} - T_{P^{\circ} P Q Q^{\circ}} . \end{matrix}

E három egyenlet alapján

\begin{matrix} T_{P Q B R} - T_{P S D T} = T_{P^{\circ} S^{\circ} S P} + T_{P^{\circ} P Q Q^{\circ}} = T_{Q Q^{\circ} S^{\circ} S}, \end{matrix}

és ezzel állításunk második részét is bebizonyítottuk.
Ha (az ábrától eltérőleg) a

P

pont az

A B C △

belsejébe esik, akkor az előbbi gondolatmenettel arra jutunk, hogy

\begin{matrix} T_{A P C P'} = T_{Q Q^{\circ} S^{\circ} S} = T_{P S D T} - T_{P Q B R} . \end{matrix}

Megemlítjük, hogy egyes versenyzők a területeket szerkesztéssel négyzetekké alakították, és ezeket hasonlították össze. Területek szemlélettel, vagy méréssel történő összehasonlítása nem tekinthető bizonyító erejűnek!