Kezdőlap


Feladat:	1958. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1958/október, 41 - 42. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Arany Dániel
Hivatkozás(ok):	Feladatok: 1958/október: 1958. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük $O B$ -nek, ill. $O C$ -nek az $A D$ -vel való metszéspontját $B_{1}$ -gyel, ill. $C_{1}$ -gyel (1. ábra).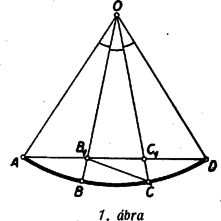

A körívet harmadoló pontokhoz húzott sugarak az

O

-nál levő középponti szöget is három egyenlő részre osztják. Húzzuk meg a

C B_{1}

szakaszt. Az így keletkezett

O C B_{1}

háromszög egybevágó az

O A B_{1}

, háromszöggel, mert annak

O B

-re vonatkozó tükörképe, ugyanis az

O A

és

O C

sugarak egyenlő szöget zárnak be

O B

-vel.
Ha megmutatjuk, hogy a

B_{1} C_{1} C

háromszögben a

C_{1}

-nél levő szög tompaszög, s így a háromszög legnagyobb szöge, ebből következni fog, hogy

B_{1} C

a háromszög leghosszabb oldala; ennek következtében

B_{1} C_{1}

kisebb

B_{1} C

-nél, tehát az utóbbival egyenlő

A B_{1}

-nél is. A két sugár a húrt ezek alapján nem osztja egyenlő részekre.
A

B_{1} C_{1} C

szög azonban az egyenlő szárú

O B_{1} C_{1}

háromszög két egyenlő szöge közül az egyiknek, tehát mindenképpen egy hegyesszögnek a kiegészítő szöge, s így valóban tompaszög. Ezzel, mint láttuk, a feladatot meg is oldottuk.
Szimmetria okokból világos, hogy a

C_{1} D

szakasz az

A B_{1}

-gyel egyenlő.

II. megoldás: Jelöljük ismét

B_{1}

-gyel és

C_{1}

-gyel az

O B

és

O C

körsugarak metszéspontját az

A D

húrral (2. ábra).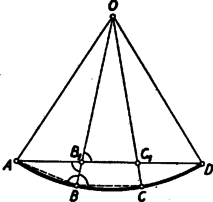

2. ábra

O B

sugár az

A B C

szög szögfelezője,

A B B_{1} ∢ = B_{1} B C ∢

. Az

A O D

szög szögfelezőjére a

B_{1}

és

C_{1}

, valamint a

B

és

C

pontok tükrös helyzetűek, így

B_{1} C_{1}

párhuzamos

B C

-vel, tehát

B_{1} B C ∢ = O B_{1} C_{1} ∢

. Az utóbbi szög csúcsszöge:

A B_{1} B

szög eszerint az

A B B_{1}

szöggel egyenlő. Az

A B B_{1}

háromszög tehát egyenlő szárú, s ezért

A B_{1} = A B

. Az

A B

mint ugyanakkora középponti szöghöz tartozó húr a

B C

húrral egyenlő. A

B O C

szög szárait metsző

B_{1} C_{1}

és

B C

párhuzamos szakaszok közül a távolabbi

B C

a hosszabb. Így az utóbbival egyenlő

A B_{1}

szakasz hosszabb, mint

B_{1} C_{1}

Megjegyzések: 1. Azok számára, akik már ismerik egy háromszög szögfelezőjének osztásarányára vonatkozó tételt (ált. gimn. II. oszt. tananyag), közöljük a feladatnak következő egyszerű megoldását.
Az

O A C_{1}

háromszögnek az

O B_{1}

szögfelezője. A szögfelezők osztásarányára vonatkozó tétel alapján

\begin{matrix} A B_{1} : B_{1} C_{1} = A O : C_{1} O . \end{matrix}

Mivel

C_{1} O

feltétlenül kisebb, mint a kör sugara, ami

A O

-val egyező nagyságú, ezért

A B_{1}

és

B_{1} C_{1}

közül a

B_{1} C_{1}

a kisebb.
2. Ha a bizonyítottakkal ellentétben az ívet harmadoló sugarak az ívhez tartozó húrt is harmadolnák, ez lehetőséget adna egy szög harmadolására körzővel és vonalzóval, ami pedig lehetetlen (l. pl. Középisk. Mat. Lapok XIV. köt. 4. és 5. sz. 97‐107. és 129‐134. o.). ‐ Sok versenyző a szögharmadolás lehetetlenségére hivatkozva cáfolta meg a keletkező szakaszok egyenlőségét. Ez a megoldás természetesen jó, de a fenti bizonyításoknál összehasonlíthatatlanul nehezebben bizonyítható, mélyebben fekvő tételt használ fel egy ilyen egyszerű feladat megoldására.