Kezdőlap


Feladat:	1958. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 1. feladata	Korcsoport: 16-17	Nehézségi fok: könnyű
Füzet:	1958/október, 40. oldal		PDF \| MathML
Témakör(ök):	Nevezetes azonosságok, Arany Dániel
Hivatkozás(ok):	Feladatok: 1958/október: 1958. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az első és második kétjegyű szám tizeseit $a$ -val, az első szám egyeseit $b$ -vel, a második szám egyeseit $c$ -vel.
A fenti számítási mód akkor helyes, ha a

\begin{matrix} (10 a + b) (10 a + c) = 10 a (10 a + c + b) + b c \end{matrix}

egyenlőség azonosság. Ez azonban igaz, mert mindkét oldal rendezett polinom alakja

\begin{matrix} 100 a^{2} + 10 a b + 10 a c + b c . \end{matrix}

Megjegyzések: 1. A

(10 a + b) (10 a + c)

és a

10 a (10 a + c + b) + b c

kifejezések egyenlőségét (tetszőleges nem negatív

a

b

c

esetén) szemléltetni is tudjuk.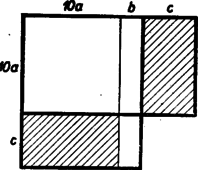

Az ábrán látható

10 a + b

és

10 a + c

oldalú téglalap területe az első kifejezést adja. A

10 a

és

10 a + b + c

oldalú téglalap területe az első téglalap területénél (a csíkozott téglalapok egybevágósága miatt) éppen egy

b

és

c

oldalú téglalap területével kevesebb.
2. A számolási eljárás változatlanul használható, ha két olyan egyenlő nagyságrendű többjegyű (esetleg tizedesjegyet is tartalmazó) számot szorzunk össze, amelynek első számjegye vagy jegyei egyenlők. Ha a két számnak ezt a közös részét jelöljük

10 a

-val, a maradék részeket

b

-vel, illetve

c

-vel, a bizonyítás változatlan marad. ‐ Ez a számolási mód többjegyű számoknál persze nem mindig jelent számítási könnyebbséget.