| Feladat: | 1957. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 3. feladata | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1957/október, 44 - 47. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Tengelyes tükrözés, Háromszögek hasonlósága, Középpontos és egyéb hasonlósági transzformációk, Arany Dániel | ||
| Hivatkozás(ok): | Feladatok: 1957/szeptember: 1957. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 3. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Készítsünk vázlatot. Legyen az adott kör középpontja , sugara , a keresett érintő kör középpontja . Ha e kör a pontban érinti az adott kör ott átmenő átmérőjét, akkor egyben érint minden olyan kört is, amelyet az átmérő -ben érint. Az átmérőt ezért egy ‐ ezek közül alkalmasan választott ‐ körrel helyettesíthetjük. 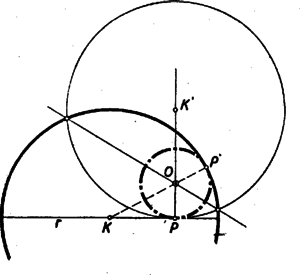 Célszerű lesz ezt a kört úgy választani, hogy az ábra szimmetrikussá váljék. Ez bekövetkezik, ha azt a kört rajzoljuk meg, amelynek sugara az adott kör sugarával egyenlő, és amelyet a keresett kör belülről érint a pontban (2. ábra). Ezután az átmérőt el is hagyhatjuk. Ezzel az ábra teljesen szimmetrikussá válik. A keresett kör középpontja rajta van az ábra szimmetria tengelyén, melyet a két egyenlő kör közös húrjaként szerkeszthetünk meg, és a -n át megrajzolt segédkör -hez vezető sugarán, amely nem más, mint a -ben az átmérőre emelt merőleges. A szerkesztés tehát a következőképpen végezhető: -ben merőlegest emelünk az átmérőre, erre rámérjük az adott kör sugarát, és a végpontból e sugárral kört rajzolunk. Ennek az adott körrel való metszéspontjait összekötő egyenes metszi ki a -ben emelt merőlegesből a keresett pontot. Valóban az körül -n át húzott kör érinti a -n átmenő átmérőt, és belülről érinti a segédkört. Így az ábra szimmetriája miatt érinti az adott kört is -ben (2. ábra). A segédkört az átmérő mindkét oldalán szerkeszthetjük, így a feladatnak két megoldása van, ha a pont és az átmérő adva van. A feladat követelményei szerint -n át átmérőt kell húzni, és azzal elvégezni a szerkesztést. Ezt az átmérőt egyértelműen meghatározza, kivéve ha a kör középpontja, amikor az átmérő tetszés szerinti irányban húzható. Utóbbi esetben tehát a feladat határozatlan, minden más esetben két megoldása van. (A versenyzők egy része minden esetben határozottnak vélte a feladatot, ez azonban a középpont megadása esetében csak akkor állna fenn, ha az átmérő előre adott volna.) II. megoldás: A feladat megoldására kínálkozik a körzsugorítás módszere. Miközben az adott kört a ponttá zsugorítjuk, az érintő kör előbb ponttá zsugorodik, majd kívülről érintő körbe megy át, és növekszik. A pont az átmérőre merőlegesen mozdul el, a ponttá zsugorított kör sugarával -be (ill. -be). A átmérő egy, a (ill. ) ponton átmenő, és az eredeti -vel párhuzamos (ill. ) egyenesbe megy át (3. ábra). 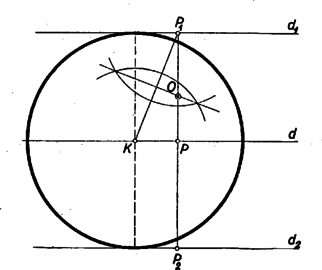 Ezzel visszavezettük a feladatot adott ponton átmenő, és adott egyenest adott pontjában érintő kör szerkesztésére, ami már ismert feladat. A keresett kör középpontját úgy kaphatjuk, mint a keresett kör két adott pontját ( és ) összekötő egyenes felező merőlegesének és az adott érintőre a érintési pontban emelt merőlegesnek metszéspontját. Ez a pont egyben az eredeti feladatban keresett kör középpontja is. Megjegyzések: 1.) Ez a megoldás szoros kapcsolatban van az előzővel. Ez világos lesz, ha észrevesszük, hogy a szakasz felező merőlegesének szerkesztéséhez tetszőleges (egyenlő) sugarú körívekül választhatjuk éppen az sugarú köríveket. Ez esetben a 3. ábra lényegében átmegy a 2. ábrába. 2.) A II. megoldás minden változtatás nélkül alkalmazható akkor is, ha a pont a körön kívül van. (Ekkor a zsugorításnál a keresett kör kezdettől fogva növekszik.) Az I. megoldás is alkalmazható ebben az esetben is, csak nem bizonyos, hogy a két egyenlő sugarú kör ekkor is metszi egymást. Ha nem, akkor a szimmetria tengelyt pl. úgy kaphatjuk, mint a két kör centrálisának felező merőlegesét. Ez ismét a két megoldás rokonságát mutatja. Az alábbi megoldások is egyaránt érvényesek a körön belül és kívül levő pontokra. Az ábrákat azonban mindig a feladat feltételeinek megfelelően készítjük. III. megoldás: Készítsünk vázlatot. Legyen az adott kör középpontja , a keresett érintő köré , a két kör érintkezési pontja . Húzzuk meg a -n át a közös érintőt és hosszabbítsuk meg az szakaszt. A két egyenes metszéspontja legyen (4. ábra). 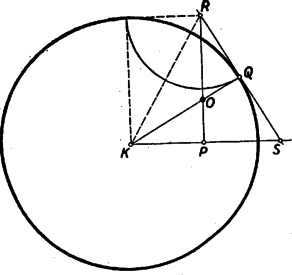 A és az háromszög derékszögű, és -nál fekvő szögeik egyenlők, mert csúcsszögek (illetőleg a körön kívüli pontra egybeesnek). Így a két háromszög hasonló. Az és oldalaik, mint az érintő kör sugarai, egyenlők, s így a két háromszög egybevágó is. Ennek folytán ‐ az adott kör sugarát -rel jelölve Ennek alapján a következő szerkesztéshez jutunk: -ben az átmérőre merőlegest állítunk, és erre rámérjük az adott kör sugarát. Megszerkesztjük ennek végpontjából húzható, és az átmérővel nem párhuzamos, érintő érintési pontját. Azt állítjuk, hogy és metszéspontja a keresett kör középpontja. Ennek igazolására jelöljük még meg az és egyenesek metszéspontját. A és háromszögek derékszögűek, -nél levő szögeik közösek (illetőleg csúcsszögek) és a szerkesztés szerint Aszerint, hogy -t az átmérő melyik oldalán szerkesztjük meg, ismét két megoldás adódik általában. IV. megoldás: A kisebbik kört a közös érintési pontból, mint nyújtási középpontból nagyítva, a kör egy-egy pontja, pl. egy -n átmenő egyenesen mozdul el. Egy-egy egyenes, pl. az körsugár, pedig önmagával párhuzamos helyzetbe megy át. Ilyen átalakítással az érintő kör átvihető az adott körbe. Eközben az átmérőre merőleges sugárba megy át (5. ábra). Ennek alapján megszerkeszthető. 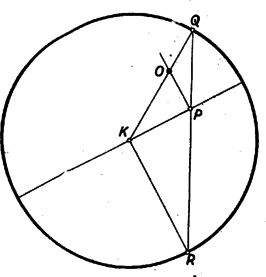 A szerkesztés menete: Az adott kör középpontjában az átmérőre állított merőleges egyik metszéspontja az adott körrel legyen , és -nek a körrel való metszéspontja . Azt állítjuk, hogy -nak és a -ben az átmérőre emelt merőlegesnek metszéspontja a keresett kör középpontja. Valóban az és háromszögek megfelelő oldalai párhuzamosak, és így megfelelő szögeik egyenlők. Az utóbbi háromszöggel együtt tehát az előbbi is egyenlő szárú: Az körül -n át húzott kör tehát átmegy -n is, és mivel ez a pont a két kör centrálisán van, így a két kör ebben a pontban érintkezik. Itt is két megoldást kapunk általában az átmérő két oldalán. |