Kezdőlap


Feladat:	1957. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1957/október, 41 - 42. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Arany Dániel
Hivatkozás(ok):	Feladatok: 1957/szeptember: 1957. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a $B C$ és $B' C'$ , a $C A$ és $C' A'$ , végül az $A B$ és $A' B'$ oldalak metszéspontját rendre $A_{1}$ , $B_{1}$ , $C_{1}$ -gyel (1. ábra).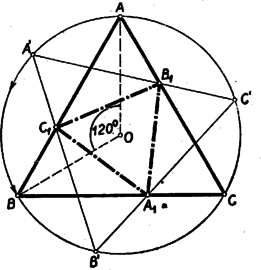

1. ábra

Ha az ábrát a kör

O

középpontja körül

120^{\circ}

-kal elforgatjuk úgy, hogy

A

B

pontba kerüljön, akkor a

B

C

A'

B'

C'

pontok rendre

C

A

B'

C'

A'

pontok helyére kerülnek. Így pl.

B C

és

B' C'

metszéspontja,

A_{1}

C A

és

C' A'

metszéspontjába

B_{1}

-be megy át, és hasonlóan a

B_{1}

és

C_{1}

pontok a

C_{1}

, ill.

A_{1}

pontok helyére kerülnek. Így

O

körüli

120^{\circ}

-os elforgatás után az

A_{1} B_{1} C_{1}

háromszög újra fedi eredeti helyzetét. Ez csak úgy lehetséges, hogy az

A_{1} B_{1} C_{1}

háromszög szabályos, és körülírt körének középpontja szintén

O

Megjegyzések: 1.) A két háromszög adott elhelyezése mellett, ha az egyik háromszöget megbetűztük, a másikat még háromféleképpen betűzhetjük meg ugyanolyan körüljárás szerint. Ha az oldalak egyeneseit tekintjük (tehát az oldalak meghosszabbításaira eső metszéspontokat is figyelembe veszünk), akkor tehát általában három háromszög kapható, mint a megfelelő oldalak metszéspontja. Ha a két háromszögnek egy oldalpárja párhuzamos, akkor a másik két oldalpár is az, s így csak két háromszög keletkezik. Ha viszont a két háromszög egybeesik, akkor az egyik (az azonos megbetűzéshez tartozó) határozatlanná válik.
2.) A bizonyításban nincs lényegesen kihasználva az sem, hogy a két háromszög ugyanabba a körbe van beírva, csak annyi, hogy a középpontjuk közös. A feladat állítása tehát igaz bármely két szabályos háromszögre, amelyeknek közös a középpontja, és amelyek egyező körüljárás szerint vannak megbetűzve.