Feladat: 1956. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 2. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1956/október, 36 - 40. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek szerkesztése, Középponti és kerületi szögek, Egyenlő szárú háromszögek geometriája, Arany Dániel
Hivatkozás(ok):Feladatok: 1956/szeptember: 1956. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek a háromszög csúcsai A, B, C, az ezeknél fekvő szögek α, β, γ. Mivel a beírt kör O középpontját a szögfelező metszéspontja adja, ezért az a=BC oldal látószöge az O pontból (3. ábra)

 
 
3. ábra
 

δ=180∘-β2-γ2=180∘-(α2+β2+γ2)+α2=90∘+α2.(1)

Ez a szög tehát α ismeretében megszerkeszthető. Azt is tudjuk, hogy O a BC oldaltól ϱ távolságra van, így a szerkesztés elvégezhető, ha a-t meg tudjuk szerkeszteni. Legyenek a beírt kör érintési pontjai a BC, CA, AB oldalon A1, B1, C1, akkor ismeretes, hogy
AB1=AC1=s-BC=s-a.(2)
(Valóban a körhöz egy pontból húzott érintő egyenlő volta miatt
s=AB1+BC1+CA1=AB1+CA1+A1B=AB1+a.)

Ezzel a következő szerkesztéshez jutottunk: Rajzoljunk α2 nagyságú szöget, csúcspontját jelöljük P-vel (4. ábra).
 
 
4. ábra
 

Húzzunk az egyik szárával párhuzamos egyenest ϱ távolságban, amely metszi a másik szárat egy Q pontban. Az előbbi szárra mérjük rá a P csúcstól a PC=s távolságot, a Q-ból PC-re bocsátott merőleges talppontja legyen B. Rajzoljuk meg azt a körívet, amelyből a BC szakasz 90∘+α2 szög alatt látszik. Messe ez az először húzott párhuzamost O és O' pontokban. Rajzoljunk pl. O körül ϱ sugarú kört. Az ehhez B-ből és C-ből húzott érintők A metszéspontja lesz a keresett háromszög harmadik csúcspontja. (E két érintő szükségképpen metszi egymást, a BC ugyanazon az oldalán, amelyen a kör van. Ugyanis ezen érintőknek a BC szakasszal bezárt, a kör oldalán fekvő szögei 2⋅OBC∢, illetőleg 2⋅OCB∢, és e két szög összege 180∘-α.)
Csak az így kapott háromszög felelhet meg a feladat feltételeinek, tehát nincs megoldása a feladatnak, ha a látókörív nem metszi a ϱ távolságban húzott párhuzamost.
Az ABC háromszög valóban megfelel a feltételeknek, mert beírt körének sugara ϱ, ennek a középpontjából a BC oldal 90+α2 szög alatt látszik, s így az A csúcsnál fekvő α' szögre (1) szerint
90∘+α'2=90∘+α2,α'=α.
Végül a beírt kör érintési pontját a CA oldalon B1-gyel jelölve, a szerkesztett háromszög s' kerületére (2) szerint
s'=AB1+BC.
De az AOB1 és PQB derékszögű háromszögek egybevágók, mert A-nál, illetőleg P-nél fekvő hegyesszögük α2, és az ezzel szemközti befogó mindkét háromszögben ϱ. Így
AB1=PB.
Ennélfogva
s'=PB+BC=s
a szerkesztés szerint.
Ha O helyett az O'-ből kiindulva fejezzük be a szerkesztést, akkor ABC-vel egybevágó megoldást kapunk, mert O és O' szimmetrikus a BC szakaszt felező merőlegesére.
 

Megjegyzés. Legyen az ABC háromszög köré írt kör A-t nem tartalmazó BC ívének felezőpontja D (5. ábr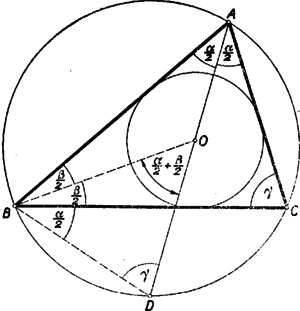a).
 
 
5. ábra
 

Tudjuk, hogy az A csúcsnál fekvő szög felezője átmegy D-n, és egyszerű szögszámítás adja, hogy a BDO háromszög egyenlő szárú: DB=DO. Így B, O és C egy D középpontú körön vannak. Ez éppen a fenti megoldásban használt látókörív.
Mivel a megszerkesztése után, α ismeretében a körülírt kör megszerkeszthető, így a D pont is. E körül B-n és C-n át körívet rajzolva, annak egyik metszéspontját a BC-től ϱ távolságra húzott párhuzamossal kössük össze D-vel. Ez metszi ki a körülírt körből A-t. Többen választották ezt a szerkesztési utat. Ehhez természetesen megfelelően kell módosítani annak bizonyítását is, hogy az ABC háromszög megfelel a feladat feltételeinek. (Lásd a jelen számban kitűzött 372. gyakorlatot.)
 

II. megoldás: Forgassuk le egy ABC háromszög oldalait pl. az AB oldal meghosszabbítására (6. ábra)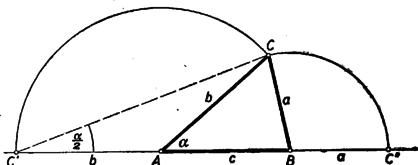
AC'=AC,BC'=BC.
 
6. ábra
 

Ha az A csúcsnál levő szög α, akkor a CAC' háromszög egyenlő szárú voltából következik, hogy
CC'A∢=CC'C''∢=α2.

Az előző megoldásban láttuk, hogy a BC=a oldal az adatokból megszerkeszthető, így megszerkeszthető a BCC' háromszög is a következő módon: Miután a-t megszerkesztettük, mint az előző megoldásban, mérjük fel egy egyenesre C'C''=2s távolságot, ennek C' végpontjában az α2 szöget, a C''-től a távolságra levő B pont körül pedig rajzoljunk a sugárral kört (7. ábra).
 
 
7. ábra
 

E körnek a szög másik szárával való valamelyik metszéspontja ‐ ha van ilyen ‐ legyen C. A CC' szakasz felező merőlegese metszi ki a C'C'' szakaszból az A pontot.
Az ABC háromszög valóban megfelel a feltételeknek, mert szerkesztés szerint a CAC' háromszög egyenlő szárú, így CA=C'A, és a háromszög A-nál levő külső szöge
CAC''∢=2⋅CC'A∢=α.

Ez az ABC háromszög belső szöge kell, hogy legyen. Ugyanis a szerkeszthetőséghez szükséges, hogy a<s legyen. Ez esetben C' az a sugarú B középpontú körön kívül van. Ha a kör és a C'C egyenes másik metszéspontját C1-gyel jelöljük, akkor a CC1 szakasz felező merőlegese B-n megy át; mivel pedig CC' (és C1C') felezőpontja C' és a C1C szakasz felezőpontja közé esik, így A-nak is C' és B közé kell esnie. CAC''∢ tehát az ABC háromszögnek valóban belső szöge. A háromszög kerülete:
CA+AB+CB=C'A+AB+BC''=2s.
Így az I. megoldás (1) szerint a beírt kör érintési pontja A-tól s-a távolságra van. Ebből, mivel a beírt kör középpontja az α szög felezőjén van, a megszerkesztése szerint következik, hogy a beírt kör sugara olyan derékszögű háromszög befogója, melynek ezzel szemközti szöge α2, a másik befogója pedig s-a. Mivel a-t egy ugyanilyen háromszög segítségével szerkesztettük, melynek emellett kérdéses befogója ϱ hosszúságú, így a megszerkesztett háromszög beírt körének sugara ϱ. A háromszög tehát megfelel a feladat feltételeinek.
Azt állítjuk, hogy ha C helyett C1-ből kiindulva szerkesztünk egy A1BC1 háromszöget, ez az előbbivel egybevágó lesz (a megfelelt csúcsok A, C és B). Valóban A1 is C' és B közé esik. Essék mondjuk a C a C' és C1 pontok közé, és jelöljük az ABC és A1BC1 háromszögek szögeit α, β, γ, illetőleg α1, β1, γ1-gyel. Szerkesztés szerint α1=α a megadott szög.
A BCC1 egyenlő szárú háromszögből
BCC1∢=BC1C∢=γ1+α2,
így a C-nél keletkező szögek összege
180∘=C'CA∢+ACB∢+BCC1∢=α2+γ+γ1+α2=α+γ+γ1,
tehát γ1=β. Az ABC és A1C1B háromszögek tehát hasonlók, mivel pedig BC és C1B oldaluk egyenlő, tehát egybevágók is.
 

III. megoldás: Rajzoljuk meg a háromszög BC oldalához hozzáírt kört is. A betűzést a 8. ábra mutatja.
 
 
8. ábra
 

Ismeretes, hogy ekkor
AB2=AC2=s.(3)
(Valóban a körhöz egy pontból húzott érintők egyenlősége folytán
2AB2=AB2+AC2=AC+CA2+AB+BA2=AC+AB+BC=2s.)

Ez a következő szerkesztéshez vezet: Szerkesszünk α nagyságú szöget, csúcsa legyen A, és szerkesszük meg a két szárat érintő ϱ sugarú k1 kört. Mérjük rá a szög egyik szárára az AC2=s távolságot, és szerkesszük meg azt a k2 kört, amelyik mindkét szárat érinti, egyiket C2-ben. Húzzuk meg a két kör egyik közös belső érintőjét, messe ez a szög szárait B és C pontokban.
ABC a keresett háromszög, mert A-nál levő szöge α, beírt körének sugara ϱ, és a (3) összefüggésből következik, hogy kerülete 2s.
A másik belső közös érintő meghúzása nyilvánvalóan a megszerkesztettel egybevágó háromszöghöz vezet.